
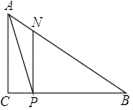
ЁОЬтФПЁПШчЭМдкЁїABCжаЃЌЁЯC=90ЁуЃЌAC=3cmЃЌBC=4cmЃЌЕуPЪЧБпBCЩЯгЩBЯђCдЫЖЏЃЈВЛгыЕуBЁЂCжиКЯЃЉЕФвЛЖЏЕуЃЌPЕуЕФЫйЖШЪЧ1cm/sЃЌЩшЕуPЕФдЫЖЏЪБМфЮЊtЃЌЙ§PЕузїACЕФЦНааЯпНЛABгыЕуNЃЌСЌНгAPЃЌ
ЃЈ1ЃЉЧыгУКЌгаtЕФДњЪ§ЪНБэЪОЯпЖЮANКЭЯпЖЮPNЕФГЄЃЌ
ЃЈ2ЃЉЕБtЮЊКЮжЕЪБЃЌЁїAPNЕФУцЛ§ЕШгкЁїACPУцЛ§ЕФШ§ЗжжЎвЛЃП
ЃЈ3ЃЉдкЕуPЕФдЫЖЏЙ§ГЬжаЃЌЪЧЗёДцдкФГвЛЪБПЬЕФtЕФжЕЃЌЪЙЕУЁїAPNЕФУцЛ§газюДѓжЕЃЌШєДцдкЧыЧѓГіtЕФжЕВЂМЦЫузюДѓУцЛ§ЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ PN=![]() tЃЌAN =5Љ
tЃЌAN =5Љ![]() tЃЛЃЈ2ЃЉЕБtЮЊ
tЃЛЃЈ2ЃЉЕБtЮЊ![]() sЪБЃЌЁїAPNЕФУцЛ§ЕШгкЁїACPУцЛ§ЕФШ§ЗжжЎвЛЃЛЃЈ3ЃЉt=2ЪБЃЌЁїPANЕФУцЛ§зюДѓЃЌзюДѓжЕЮЊ
sЪБЃЌЁїAPNЕФУцЛ§ЕШгкЁїACPУцЛ§ЕФШ§ЗжжЎвЛЃЛЃЈ3ЃЉt=2ЪБЃЌЁїPANЕФУцЛ§зюДѓЃЌзюДѓжЕЮЊ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУЙДЙЩЖЈРэЧѓГіABЃЌдйРћгУЦНааЯпЗжЯпЖЮГЩБШР§ЖЈРэЃЌЧѓГіPNЁЂBNМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉгЩЬтвтЃК![]() PNPCЃН
PNPCЃН![]() ЁС
ЁС![]() PCACЃЌЭЦГіACЃН3PNЃЌгЩДЫЙЙНЈЗНГЬМДПЩНтОіЮЪЬтЃЛ
PCACЃЌЭЦГіACЃН3PNЃЌгЩДЫЙЙНЈЗНГЬМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉЙЙНЈЖўДЮКЏЪ§ЃЌРћгУЖўДЮКЏЪ§ЕФаджЪМДПЩНтОіЮЪЬт.
ЃЈ1ЃЉдкRtЁїABCжаЃЌЁпЁЯC=90ЁуЃЌAC=3cmЃЌBC=4cmЃЌ
ЁрAB=![]() =5ЃЈcmЃЉЃЌ
=5ЃЈcmЃЉЃЌ
ЁпPNЁЮACЃЌPB=tЃЌ
Ёр![]() =
=![]() =
=![]() ЃЌ
ЃЌ
Ёр![]() =
=![]() =
=![]() ЃЌ
ЃЌ
ЁрBN=![]() tЃЌPN=
tЃЌPN=![]() tЃЌ
tЃЌ
ЁрAN=ABЉBN=5Љ![]() tЃЎ
tЃЎ
ЃЈ2ЃЉгЩЬтвтЃК![]() PNPC=
PNPC=![]() ЁС
ЁС![]() PCACЃЌ
PCACЃЌ
ЁрAC=3PNЃЌ
Ёр3=3![]() tЃЌ
tЃЌ
Ёрt=![]() ЃЌ
ЃЌ
ЁрЕБtЮЊ2sЪБЃЌЁїAPNЕФУцЛ§ЕШгкЁїACPУцЛ§ЕФШ§ЗжжЎвЛЃЎ
ЃЈ3ЃЉгЩЬтвтЃКSЁїAPN=![]() PNPC=
PNPC=![]()
![]() tЃЈ4ЉtЃЉ=Љ
tЃЈ4ЉtЃЉ=Љ![]() ЃЈtЉ2ЃЉ2+
ЃЈtЉ2ЃЉ2+![]() ЃЌ
ЃЌ
ЁпЉ![]() ЃМ0ЃЌ
ЃМ0ЃЌ
Ёрt=2ЪБЃЌЁїPANЕФУцЛ§зюДѓЃЌзюДѓжЕЮЊ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉШчЭМЃЈ1ЃЉЃЌвбжЊЃКдкЁїABCжаЃЌЁЯBACЃН90ЁуЃЌAB=ACЃЌжБЯпmОЙ§ЕуAЃЌBDЁЭжБЯпm, CEЁЭжБЯпm,ДЙзуЗжБ№ЮЊЕуDЁЂE.жЄУї:DE=BD+CE.
ЃЈ2ЃЉ ШчЭМЃЈ2ЃЉЃЌНЋЃЈ1ЃЉжаЕФЬѕМўИФЮЊЃКдкЁїABCжаЃЌAB=ACЃЌDЁЂAЁЂEШ§ЕуЖМдкжБЯпmЩЯ,ВЂЧвгаЁЯBDA=ЁЯAEC=ЁЯBAC=![]() ,Цфжа
,Цфжа![]() ЮЊШЮвтШёНЧЛђЖлНЧ.ЧыЮЪНсТлDE=BD+CEЪЧЗёГЩСЂ?ШчГЩСЂ,ЧыФуИјГіжЄУї;ШєВЛГЩСЂ,ЧыЫЕУїРэгЩ.
ЮЊШЮвтШёНЧЛђЖлНЧ.ЧыЮЪНсТлDE=BD+CEЪЧЗёГЩСЂ?ШчГЩСЂ,ЧыФуИјГіжЄУї;ШєВЛГЩСЂ,ЧыЫЕУїРэгЩ.
ЃЈ3ЃЉЭиеЙгыгІгУЃКШчЭМЃЈ3ЃЉЃЌDЁЂEЪЧDЁЂAЁЂEШ§ЕуЫљдкжБЯпmЩЯЕФСНЖЏЕуЃЈDЁЂAЁЂEШ§ЕуЛЅВЛжиКЯЃЉ,ЕуFЮЊЁЯBACЦНЗжЯпЩЯЕФвЛЕу,ЧвЁїABFКЭЁїACFОљЮЊЕШБпШ§НЧаЮЃЌСЌНгBDЁЂCE,ШєЁЯBDA=ЁЯAEC=ЁЯBACЃЌЪдХаЖЯЁїDEFЕФаЮзД.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдквЛПУЪїCDЕФ10mИпДІЕФBЕугаСНжЛКязгЃЌЫќУЧЖМвЊЕНAДІГиЬСБпКШЫЎЃЌЦфжавЛжЛКязгбиЪїХРЯТзпЕНРыЪї20mДІЕФГиЬСAДІЃЌСэвЛжЛКязгХРЕНЪїЖЅDКѓжБЯпдОШыГиЬСЕФAДІЃЎШчЙћСНжЛКязгЫљОЙ§ЕФТЗГЬЯрЕШЃЌЪдЮЪетПУЪїЖрИпЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкБпГЄЮЊ1ИіЕЅЮЛГЄЖШЕФаЁе§ЗНаЮзщГЩЕФЭјИёжаЃЌЕуAЁЂBЁЂCдкаЁе§ЗНаЮЕФЖЅЕуЩЯ.
(1)дкЭМжаЛГігыЁїABCЙигкжБЯпlГЩжсЖдГЦЕФЁїAЁфBЁфCЁф.
(2)ЫФБпаЮ ABCAЁфЕФУцЛ§ЮЊ_____ЃЛ
(3)дкжБЯпlЩЯеввЛЕуPЃЌЪЙPA+PBЕФГЄзюЖЬЃЌдђетИізюЖЬГЄЖШЮЊ______.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЃЌДгЯТСаЬѕМўжаВЙГфвЛИіЬѕМўКѓЃЌШдВЛФмХаЖЈ
ЃЌДгЯТСаЬѕМўжаВЙГфвЛИіЬѕМўКѓЃЌШдВЛФмХаЖЈ![]() ЕФЪЧ( )
ЕФЪЧ( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕжаЃЌжБЯпy=![]() x+4
x+4![]() ЗжБ№НЛxжсЁЂyжсгкЕуAЁЂCЃЌжБЯпBCгыжБЯпACЙигкyжсЖдГЦЃЌЖЏЕуDДгЕуAГіЗЂЃЌбиACвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШЯђжеЕуCдЫЖЏЃЌЕБЕуDГіЗЂКѓЃЌЙ§ЕуDзїDEЁЮBCНЛелЯпAЉOЉCгкЕуEЃЌвдDEЮЊБпзїЕШБпЁїDEFЃЌЩшЁїDEFгыЁїACOжиЕўВПЗжЭМаЮЕФУцЛ§ЮЊSЃЌЕуDдЫЖЏЕФЪБМфЮЊtУыЃЎ
ЗжБ№НЛxжсЁЂyжсгкЕуAЁЂCЃЌжБЯпBCгыжБЯпACЙигкyжсЖдГЦЃЌЖЏЕуDДгЕуAГіЗЂЃЌбиACвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШЯђжеЕуCдЫЖЏЃЌЕБЕуDГіЗЂКѓЃЌЙ§ЕуDзїDEЁЮBCНЛелЯпAЉOЉCгкЕуEЃЌвдDEЮЊБпзїЕШБпЁїDEFЃЌЩшЁїDEFгыЁїACOжиЕўВПЗжЭМаЮЕФУцЛ§ЮЊSЃЌЕуDдЫЖЏЕФЪБМфЮЊtУыЃЎ
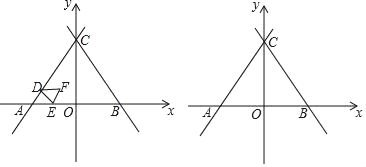
ЃЈ1ЃЉаДГізјБъЃКЕуAЃЈ ЁЁЃЉЃЌЕуBЃЈЁЁ ЁЁЃЉЃЌЕуCЃЈЁЁ ЁЁЃЉЃЛ
ЃЈ2ЃЉЕБЕуEдкЯпЖЮAOЩЯЪБЃЌЧѓSгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉЧѓГівдЕуBЁЂEЁЂFЮЊЖЅЕуЕФШ§НЧаЮЪЧжБНЧШ§НЧаЮЪБtЕФжЕЃЛ
ЃЈ4ЃЉжБНгаДГіЕуFдЫЖЏЕФТЗГЬГЄЮЊЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуPЃЌQЪЧжБЯпy=![]() x+2ЩЯЕФСНЕуЃЌЕуPдкЕуQЕФзѓВрЃЌЧвТњзуOP=OQЃЌOPЁЭOQЃЌдђЕуQЕФзјБъЪЧ______.
x+2ЩЯЕФСНЕуЃЌЕуPдкЕуQЕФзѓВрЃЌЧвТњзуOP=OQЃЌOPЁЭOQЃЌдђЕуQЕФзјБъЪЧ______.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
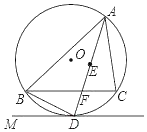
ЁОЬтФПЁПШчЭМЃЌЁбOЪЧЁїABCЕФЭтНгдВЃЌЕуEЮЊЁїABCФкЧадВЕФдВаФЃЌСЌНгAEЕФбгГЄЯпНЛBCгкЕуFЃЌНЛЁбOгкЕуDЃЛСЌНгBDЃЌЙ§ЕуDзїжБЯпDMЃЌЪЙЁЯBDM=ЁЯDACЃЎ
ЃЈ1ЃЉЧѓжЄЃКжБЯпDMЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєDF=2ЃЌЧвAF=4ЃЌЧѓBDКЭDEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
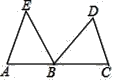
ЁОЬтФПЁПШчЭМЃЌдкЁїABEжаЃЌCЮЊБпABбгГЄЯпЩЯвЛЕуЃЌBC=AEЃЌЕуDдкЁЯEBCФкВПЃЌЧвЁЯEBD=ЁЯA=ЁЯDCBЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїABEЁеЁїCDBЃЎ
ЃЈ2ЃЉСЌНсDEЃЌШєЁЯCDB=60ЁуЃЌЁЯAEB=50ЁуЃЌЧѓЁЯBDEЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com