‘ƒ∂¡œ¬¡–≤ƒ¡œ£∫
–°√˜”ˆµΩ’‚—˘“ª∏ˆŒ £∫“—÷™£∫‘⁄°˜ABC÷–£¨AB£¨BC£¨AC»˝±þµƒ≥§∑÷±Œ™
°¢
°¢
£¨«Û°˜ABCµƒ√ʪ˝£Æ
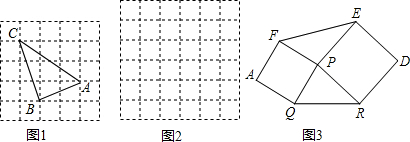
–°√˜ «’‚—˘Ω‚戌 µƒ£∫»ÁÕº1À˘ 棨œ»ª≠“ª∏ˆ’˝∑Ω–ŒÕ¯∏Ò£®√ø∏ˆ–°’˝∑Ω–Œµƒ±þ≥§Œ™1£©£¨‘Ÿ‘⁄Õ¯∏Ò÷–ª≠≥ˆ∏Òµ„°˜ABC£®º¥°˜ABC»˝∏ˆ∂•µ„∂º‘⁄–°’˝∑Ω–Œµƒ∂•µ„¥¶£©£¨¥”∂¯ΩË÷˙Õ¯∏ÒæՃк∆À„≥ˆ°˜ABCµƒ√ʪ˝£ÆÀ˚∞—’‚÷÷Ω‚æˆŒ µƒ∑Ω∑®≥∆Œ™ππÕº∑®£Æ
«Îªÿ¥£∫
£®1£©Õº1÷–°˜ABCµƒ√ʪ˝Œ™
£ª
≤Œøº–°√˜Ω‚戌 µƒ∑Ω∑®£¨ÕÍ≥…œ¬¡–Œ £∫
£®2£©Õº2 «“ª∏ˆ6°¡6µƒ’˝∑Ω–ŒÕ¯∏Ò£®√ø∏ˆ–°’˝∑Ω–Œµƒ±þ≥§Œ™1£©£Æ
¢Ÿ¿˚”√ππÕº∑®‘⁄¥Ã‚ø®µƒÕº2÷–ª≠≥ˆ»˝±þ≥§∑÷±Œ™
°¢
2°¢
µƒ∏Òµ„°˜DEF£ª
¢⁄º∆À„°˜DEFµƒ√ʪ˝Œ™
£Æ
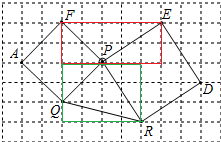
£®3£©»ÁÕº3£¨“—÷™°˜PQR£¨“‘PQ£¨PRŒ™±þœÚÕ‚◊˜’˝∑Ω–ŒPQAF£¨PRDE£¨¡¨Ω”EF£Æ»ÙPQ=
2£¨PR=
£¨QR=
£¨‘Ú¡˘±þ–ŒAQRDEFµƒ√ʪ˝Œ™
£Æ






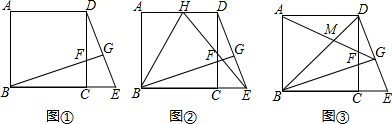
 »ÁÕº£¨÷±œþAC°ŒBD£¨÷±œþAB∑÷±”ÎÀ¸√«œýΩª”⁄A£¨B£¨»˝Ãı÷±œþ∞—∆Ω√Ê∑÷≥…¢Ÿ¢⁄¢€¢Ð¢ð¢Þ¡˘∏ˆ≤ø∑÷£®√ø∏ˆ≤ø∑÷≤ª∞¸¿®±þΩÁ£©£Æµ±∂ص„P¬‰‘⁄ƒ≥∏ˆ≤ø∑÷ ±£¨¡¨Ω·PA£¨PB£¨ππ≥…°œPAC£¨°œAPB£¨°œPBD»˝∏ˆΩ«£Æ
»ÁÕº£¨÷±œþAC°ŒBD£¨÷±œþAB∑÷±”ÎÀ¸√«œýΩª”⁄A£¨B£¨»˝Ãı÷±œþ∞—∆Ω√Ê∑÷≥…¢Ÿ¢⁄¢€¢Ð¢ð¢Þ¡˘∏ˆ≤ø∑÷£®√ø∏ˆ≤ø∑÷≤ª∞¸¿®±þΩÁ£©£Æµ±∂ص„P¬‰‘⁄ƒ≥∏ˆ≤ø∑÷ ±£¨¡¨Ω·PA£¨PB£¨ππ≥…°œPAC£¨°œAPB£¨°œPBD»˝∏ˆΩ«£Æ