Question

【题目】已知关于， 的方程组

（1）请写出方程的所有正整数解；

（2）若方程组的解满足，求的值；

（3）无论实数取何值，方程总有一个公共解，你能把求出这个公共解吗？

（4）如果方程组有整数解，求整数的值。

Answer 1

【答案】(1) ; ;(2) ;(3)x=0,y=;(4)2或-6.

【解析】试题分析：（1）由题意求方程的解且要使x，y都是正整数，将方程移项，再把x和y互相表示出来，在由题意要求x＞0，y＞0，根据以上两个条件可夹出合适的x值,从而代入方程得到相应的y值；

（2）由方程组求得x，y的值，代入方程即可求得m的值；

（3）方程整理后，根据无论m如何变化，二元一次方程总有一个固定的解，列出方程组，求出方程组的解即可．

（4）先把m当作已知求出x、y的值，再根据方程组有正整数解，进行判断，再找出符合条件的正整数m的值即可．

试题解析（1）由已知方程x+2y=5，移项得x=5-2y，

∵x，y都是正整数，则有x=5-2y＞0，又∵x＞0，

∴0＜y＜2.5，

又∵y为正整数，根据以上条件可知，合适的y值只能是y=1、2，

代入方程得相应x=3、1，

∴方程2x+y=5的正整数解为；

(2) ∵x+y=0

∴x+2y=5变为y=5

∴x=-5

将代入得.

(3) ∵由题意得二元一次方程总有一个公共解

∴方程变为(m+1)x-2y+9=0

∵这个解和m无关，

∴x=0，y=

(4) 将方程组两个方程相加得

∴

∵方程组有整数解且m为整数

∴， ，

①m+2=1，计算得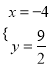： （不符合题意）

②m+2=-1，计算得： （不符合题意）

③m+2=2，计算得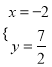： （不符合题意）

④m+2=-2，计算得： （不符合题意）

⑤m+2=4，计算得： （不符合题意）∴m=2

⑥ m+2=-4，计算得： （不符合题意）∴m=-6