
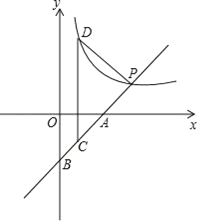
【题目】如图,直线AB交x轴于点A(4,0),交y轴于点B,交反比例函数y=![]() (k≠0)于点P(第一象限),若点P的纵坐标为2,且tan∠BAO=1
(k≠0)于点P(第一象限),若点P的纵坐标为2,且tan∠BAO=1
(1)求出反比例函数y=![]() (k≠0)的解析式;
(k≠0)的解析式;
(2)过线段AB上一点C作x轴的垂线,交反比例函数y=![]() (k≠0)于点D,连接PD,当△CDP为等腰三角形时,求点C的坐标.
(k≠0)于点D,连接PD,当△CDP为等腰三角形时,求点C的坐标.
【答案】(1)y=![]() (2)当C(2,-2)时,△CDP为等腰直角三角形
(2)当C(2,-2)时,△CDP为等腰直角三角形
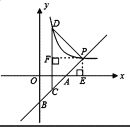
【解析】试题分析:(1)过P作PE⊥x轴于点E,求出点P的坐标,进而求出反比例函数的解析式;
(2)首先求出直线AB的解析式,然后设C(m,m-4),则D(m, ![]() ),过P作PF⊥CD于F.则F(m,2),则F(m,2),根据DF=CF列出m的方程求出m即可.
),过P作PF⊥CD于F.则F(m,2),则F(m,2),根据DF=CF列出m的方程求出m即可.
试题解析:(1)过P作PE⊥x轴于点E,∵tan∠BAO=1,∴∠BAO=45°,
∴∠BAO=∠ABO=∠PAE=45°
∵点P的纵坐标为2,∴PE=AE=2,∵A(4,0),∴P(6,2)
把点P代人y=![]() 得k=12.∴反比例函数的解析式为y=
得k=12.∴反比例函数的解析式为y=![]()
(2)设直线AB的解析式为y=kx+b且过A(4,0),P(6,2)
![]() ,解得
,解得![]() ,∴y=x-4
,∴y=x-4
要使△CDP是等腰直角三角形,只能∠DPC=90°,
设C(m,m-4),则D(m, ![]() ).过P作PF⊥CD于F.则F(m,2),
).过P作PF⊥CD于F.则F(m,2),
∴PD=PC,PF⊥CD,∴DF=CF,∴![]() -2=2-(m-4),
-2=2-(m-4),
∴m2-8m+12=0,(m-2)(m-6)=0,∴m1=2,m2=6(不合题意,舍去),
∴当C(2,-2)时,△CDP为等腰直角三角形。


科目:初中数学 来源: 题型:
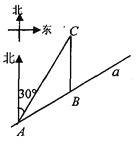
【题目】如图,某市郊外景区内一条笔直的公路a经过A、B两个景点,景区管委会又开发了风景优美的景点C,经测量景点C位于景点A的北偏东30°方向8km处,位于景点B的正北方向,已知AB=5km.
(1)求景点B与景点为C的距离;(结果保留根号)
(2)为方便游客到景点游玩,景区管委会准备由景点C向公路a修建一条距离最短的公路,不考虑其它因素,求出这条公路的长.(结果精确到0.1km.参考数据: ![]() =1.73,
=1.73, ![]() =2.24)
=2.24)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是根据宝塔山公园的平面示意图建立的平面直角坐标系,公园的入口位于坐标原点O,古塔位于点A(﹣400,300),从古塔出发沿射线OA方向前行300m是盆景园B,从盆景园B向右转90°后直行400m到达樱花园C,则点C的坐标是 . 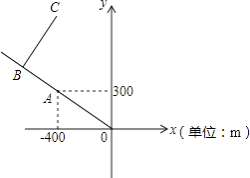
查看答案和解析>>
科目:初中数学 来源: 题型:
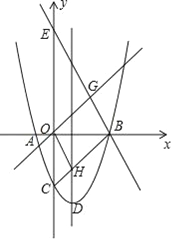
【题目】如图,抛物线y=x2﹣(m+2)x+3(m﹣1)与x轴的两个交点为A、B,与y轴交于点C,点D为抛物线的顶点,直线y=﹣2x+m+6经过点B,交y轴于点E(0,6).
(1)求直线和抛物线的解析式;
(2)如果抛物线的对称轴与线段BC交于点H,且直线y=x与直线y=﹣2x+m+6交于点G,求证:四边形OHBG是平行四边形;
(3)在抛物线上是否存在点P,使△APB的面积等于平行四边形OHBG的面积,若存在,直接写出P点的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解大气污染情况,某学校兴趣小组搜集了20I7年上半年中120天郑州市的空气质量指数,绘制了如下不完整的统计图表:
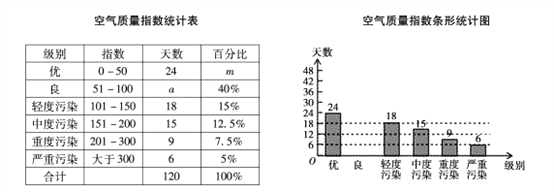
请根据图表中提供的信息,解答下面的问题:
(1)空气质量指数统计表中的a=_________,m=_________;
(2)请把空气质量指数条形统计图补充完整;
(3)若绘制“空气质量指数扇形统计图”,级别为“优”所对应扇形的圆心角是_________。
(4)请通过计算估计郑州市2017年(365)天冲空气质量指数大于100的天数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC≌△DCB,若BC=10cm,AB=6cm,AC=7cm,则CD为( )
A. 10cm B. 7cm C. 6cm D. 6cm或7cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com