
【题目】如图,某市郊外景区内一条笔直的公路a经过A、B两个景点,景区管委会又开发了风景优美的景点C,经测量景点C位于景点A的北偏东30°方向8km处,位于景点B的正北方向,已知AB=5km.
(1)求景点B与景点为C的距离;(结果保留根号)
(2)为方便游客到景点游玩,景区管委会准备由景点C向公路a修建一条距离最短的公路,不考虑其它因素,求出这条公路的长.(结果精确到0.1km.参考数据: ![]() =1.73,
=1.73, ![]() =2.24)
=2.24)
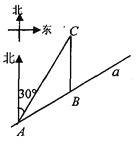
【答案】(1)景点B与景点为C的距离为(![]() 3)km;(2)这条公路长约为3.1km.
3)km;(2)这条公路长约为3.1km.
【解析】试题分析:(1)过点A作AD⊥CB,交CB的延长线于点D,先解Rt△ADC,得出CD=4![]() ,再解Rt△ABD,得出BD=3,则BC=CD-BD;(2)过点C作CE⊥AB于点E.在Rt△CBE中,由正弦函数的定义即可求解.
,再解Rt△ABD,得出BD=3,则BC=CD-BD;(2)过点C作CE⊥AB于点E.在Rt△CBE中,由正弦函数的定义即可求解.
试题解析:(1)如图,过点A作AD⊥CB,交CB的延长线于点D.
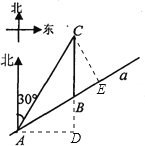
在Rt△ADC中,∠ADC=90°,∠ACD=30°,
∴AD=![]() AC=
AC=![]() ×8=4,
×8=4,
∴CD=![]() .
.
在Rt△ABD中,BD=![]() ,
,
∴BC=CDBD=![]() 3,
3,
答:景点B与景点为C的距离为(![]() 3)km;
3)km;
(2)过点C作CE⊥AB于点E.sin∠ABD=![]() .
.
在Rt△CBE中,sin∠CBE=![]() ,
,
∵∠ABD=∠CBE,
∴sin∠CBE=![]() ,
,
∴CE=CBsin∠CBE=(![]() 3)×
3)×![]() =
=![]() ≈3.1(km).
≈3.1(km).
答:这条公路长约为3.1km.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】探索函数![]() 的图象和性质.
的图象和性质.
已知函数y=x(x>0)和![]() 的图象如图所示,若P为函数
的图象如图所示,若P为函数![]() 图象上的点,过P作PC垂直于x轴且与直线、双曲线、x轴分别交于点A、B、C,则PC=
图象上的点,过P作PC垂直于x轴且与直线、双曲线、x轴分别交于点A、B、C,则PC= ![]() =AC+BC,从而“点P可以看作点A的沿竖直方向向上平移BC个长度单位(PA=BC)而得到”.
=AC+BC,从而“点P可以看作点A的沿竖直方向向上平移BC个长度单位(PA=BC)而得到”.
(1)根据以上结论,请在下图中作出函数![]() 图象上的一些点,并画出该函数的图象.
图象上的一些点,并画出该函数的图象.
(2)观察图象,写出函数![]() 两条不同类型的性质.
两条不同类型的性质.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中是假命题的是( )
A. 平面内,垂直于同一条直线的两条直线平行;
B. 同旁内角互补;
C. 等角的余角相等;
D. 互为补角的两个角不都是锐角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在一条长400米的直线跑道上同起点、同终点、同方向匀速跑步,先到终点的人原地休息.已知甲先出发3秒,在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,则下列结论正确的个数有( )
①乙的速度是4米/秒;
②离开起点后,甲、乙两人第一次相遇时,距离起点12米;
③甲从起点到终点共用时83秒;
④乙到达终点时,甲、乙两人相距68米;
⑤乙离开起点12秒后,甲乙第一次相遇.
A.4个
B.3个’
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与反比例函数
,与反比例函数![]() 的图象交于点
的图象交于点![]() .
.
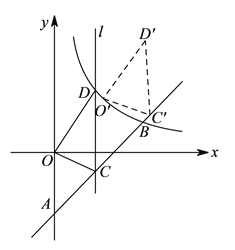
(![]() )
)![]() __________;
__________;![]() __________.
__________.
(![]() )点
)点![]() 是直线
是直线![]() 上的动点(与点
上的动点(与点![]() ,
,![]() 不重合),过点
不重合),过点![]() 且平行于
且平行于![]() 轴的直线
轴的直线![]() 交这个反比例函数的图象于点
交这个反比例函数的图象于点![]() ,当点
,当点![]() 的横坐标为
的横坐标为![]() 时,得
时,得![]() ,现将
,现将![]() 沿射线
沿射线![]() 方向平移一定的距离(如图),得到
方向平移一定的距离(如图),得到![]() ,若点
,若点![]() 的对应点
的对应点![]() 落在该反比例函数图象上,求点
落在该反比例函数图象上,求点![]() ,
,![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB交x轴于点A(4,0),交y轴于点B,交反比例函数y=![]() (k≠0)于点P(第一象限),若点P的纵坐标为2,且tan∠BAO=1
(k≠0)于点P(第一象限),若点P的纵坐标为2,且tan∠BAO=1
(1)求出反比例函数y=![]() (k≠0)的解析式;
(k≠0)的解析式;
(2)过线段AB上一点C作x轴的垂线,交反比例函数y=![]() (k≠0)于点D,连接PD,当△CDP为等腰三角形时,求点C的坐标.
(k≠0)于点D,连接PD,当△CDP为等腰三角形时,求点C的坐标.
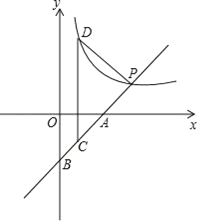
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com