
【题目】甲、乙两人在一条长400米的直线跑道上同起点、同终点、同方向匀速跑步,先到终点的人原地休息.已知甲先出发3秒,在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,则下列结论正确的个数有( )
①乙的速度是4米/秒;
②离开起点后,甲、乙两人第一次相遇时,距离起点12米;
③甲从起点到终点共用时83秒;
④乙到达终点时,甲、乙两人相距68米;
⑤乙离开起点12秒后,甲乙第一次相遇.
A.4个
B.3个’
C.2个
D.1个
【答案】C
【解析】解 :由函数图象,得:甲的速度为12÷3=4米/秒,乙的速度为400÷80=5米/秒,故①不符合题意;
设乙离开起点x秒后,甲、乙两人第一次相遇,根据题意得:
5x=12+4x,
解得:x=12,
∴离开起点后,甲、乙两人第一次相遇时,距离起点为:12×5=60(米),故②不符合题意,故⑤符合题意;
甲从起点到终点共用时为:400÷4=100(秒),故③不符合题意;
∵乙到达终点时,所用时间为80秒,甲先出发3秒,
∴此时甲行走的时间为83秒,
∴甲走的路程为:83×4=332(米),
∴乙到达终点时,甲、乙两人相距:400332=68(米),故④符合题意;
故答案为:C .
通过函数图象可得,甲出发3秒走的路程为12米,乙到达终点所用的时间为80秒,根据行程问题的数量关系可以求出甲、乙的速度,利用数形结合思想及一元一次方程即可求出甲乙第一次相遇时,乙出发的时间,乙到达终点时甲离终点的距离,及甲行完全程所用的时间,从而能做出判断得出答案。


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.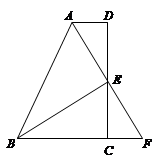
求证:
(1)AD=FC;
(2)AB=BC+AD
查看答案和解析>>
科目:初中数学 来源: 题型:
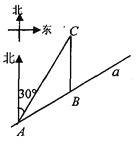
【题目】如图,某市郊外景区内一条笔直的公路a经过A、B两个景点,景区管委会又开发了风景优美的景点C,经测量景点C位于景点A的北偏东30°方向8km处,位于景点B的正北方向,已知AB=5km.
(1)求景点B与景点为C的距离;(结果保留根号)
(2)为方便游客到景点游玩,景区管委会准备由景点C向公路a修建一条距离最短的公路,不考虑其它因素,求出这条公路的长.(结果精确到0.1km.参考数据: ![]() =1.73,
=1.73, ![]() =2.24)
=2.24)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中, ![]() C=2
C=2 ![]() B,点D是BC上一点,AD=6,且AD
B,点D是BC上一点,AD=6,且AD ![]() AB,点E是BD上的点,AE=
AB,点E是BD上的点,AE= ![]() BD,AC=5,贝AB的长度为 .
BD,AC=5,贝AB的长度为 . 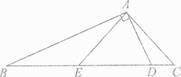
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB:y=一 ![]() x+2与x轴相交于点A,与y轴交于点B.直线CD:y=kx+b经过点c(一1,0),D(0,
x+2与x轴相交于点A,与y轴交于点B.直线CD:y=kx+b经过点c(一1,0),D(0, ![]() ),与直线AB交于点E.
),与直线AB交于点E.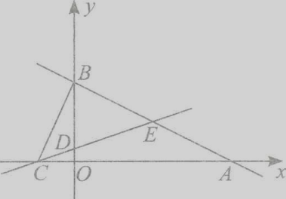
(1)求直线CD的函数关系式;
(2)连接BC,求△BCE的面积;
(3)设点Q的坐标为(m,2),求m的值使得QA+QE值最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是根据宝塔山公园的平面示意图建立的平面直角坐标系,公园的入口位于坐标原点O,古塔位于点A(﹣400,300),从古塔出发沿射线OA方向前行300m是盆景园B,从盆景园B向右转90°后直行400m到达樱花园C,则点C的坐标是 . 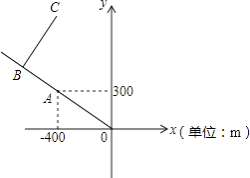
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC≌△DCB,若BC=10cm,AB=6cm,AC=7cm,则CD为( )
A. 10cm B. 7cm C. 6cm D. 6cm或7cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com