
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.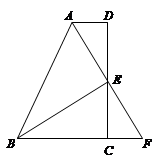
求证:
(1)AD=FC;
(2)AB=BC+AD
【答案】
(1)证明:∵AD∥BC,
∴![]() ADC=
ADC=![]() ECF,
ECF,
∵E是CD的中点,
∴DE=EC,
在![]() ADE和
ADE和![]() FCE中,
FCE中, ,
,
∴![]() ADE
ADE![]()
![]() FCE(ASA),
FCE(ASA),
∴AD=FC.
(2)证明:∵![]() ADE
ADE![]()
![]() FCE,
FCE,
∴AE=EF,AD=CF,
∴BE是线段AF的垂直平分线,
∴AB=BF=BC+CF,
∵AD=CF,
∴AB=BC+AD.
【解析】(1)根据AD∥BC可知![]() ADC=
ADC=![]() ECF,再根据E是CD的中点可证出
ECF,再根据E是CD的中点可证出![]() ADE
ADE![]()
![]() FCE,进而根据全等三角形的性质即可解答;(2)根据线段垂直平分线的性质判断出AB=BF即可.
FCE,进而根据全等三角形的性质即可解答;(2)根据线段垂直平分线的性质判断出AB=BF即可.
【考点精析】解答此题的关键在于理解线段垂直平分线的性质的相关知识,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等.


科目:初中数学 来源: 题型:
【题目】已知一次函数y=﹣ ![]() x+2和y=2x﹣3的图象分别交y轴与A、B两点,两个一次函数的图象相交于点P.
x+2和y=2x﹣3的图象分别交y轴与A、B两点,两个一次函数的图象相交于点P.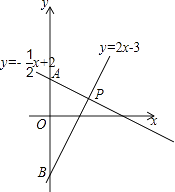
(1)求△PAB的面积;
(2)求证:∠APB=90°;
(3)若在一次函数y=2x﹣3的图象上有一点N,且横坐标为x,连结NA,请直接写出△NAP的面积关于x的函数关系式,并写出相应x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着车辆的增加,交通违规的现象越来越严重,交警对人民路某雷达测速区检测到的一组汽车的时速数据进行整理(速度在30﹣40含起点值30,不含终点值40),得到其频数及频率如表: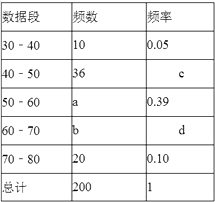
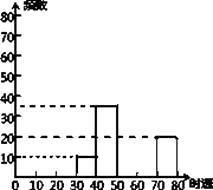
(1)表中a、b、c、d分别为:a=; b=; c=; d=.
(2)补全频数分布直方图;
(3)如果某天该路段约有1500辆通过,汽车时速不低于60千米即为违章,通过该统计数据估计当天违章车辆约有多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=BC=CD=AD,∠BAD=∠B=∠C=∠D=90°,点E、F分别在正方形ABCD的边DC、BC上,AG⊥EF且 AG=AB,垂足为G,则: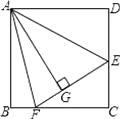
(1)△ABF与△ AGF全等吗?说明理由;
(2)求∠EAF的度数;
(3)若AG=4,△AEF的面积是6,求△CEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D是等边△ABC中BC边上一点,过点D分别作DE∥AB,DF∥AC,交AC,AB于E,F,连接BE,CF,分别交DF,DE于点N,M,连接MN.试判断△DMN的形状,并说明理由.
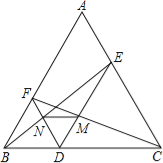
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用甲、乙两种原料配制某种饮料,这两种原料的维生素C含量及购买两种原料的价格如表:
原料 | 甲 | 乙 |
维生素C的含量/(单位/kg) | 600 | 100 |
原料价格/(元/kg) | 8 | 4 |
现配制这种饮料10千克,要求至少含有4200单位的维生素C,且购买甲、乙两种原料的费用不超过72元,求所需甲种原料的质量应满足的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在一条长400米的直线跑道上同起点、同终点、同方向匀速跑步,先到终点的人原地休息.已知甲先出发3秒,在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,则下列结论正确的个数有( )
①乙的速度是4米/秒;
②离开起点后,甲、乙两人第一次相遇时,距离起点12米;
③甲从起点到终点共用时83秒;
④乙到达终点时,甲、乙两人相距68米;
⑤乙离开起点12秒后,甲乙第一次相遇.
A.4个
B.3个’
C.2个
D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com