
【题目】如图,在正方形ABCD中,AB=BC=CD=AD,∠BAD=∠B=∠C=∠D=90°,点E、F分别在正方形ABCD的边DC、BC上,AG⊥EF且 AG=AB,垂足为G,则: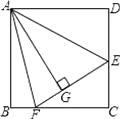
(1)△ABF与△ AGF全等吗?说明理由;
(2)求∠EAF的度数;
(3)若AG=4,△AEF的面积是6,求△CEF的面积.
【答案】
(1)解:△ABF与△ AGF全等,理由如下:
在Rt![]() ABF和Rt
ABF和Rt![]() AGF中,
AGF中,![]() ,
,
∴△ABF![]() △ AGF.
△ AGF.
(2)解:∵△ABF![]() △ AGF,
△ AGF,
∴![]() BAF=
BAF=![]() GAF,
GAF,
同理易得:△AGE![]() △ ADE,有
△ ADE,有![]() GAE=
GAE=![]() DAE,
DAE,
即![]() EAF=
EAF=![]() EAD+
EAD+![]() FAG=
FAG=![]()
![]() BAD=45
BAD=45![]() .
.
(3)解:∵S![]() AEF=
AEF=![]()
![]() EF
EF![]() AG,AG=4,
AG,AG=4,
∴6=![]()
![]() EF
EF![]() AG,
AG,
∴EF=3,
∵BF=FG,EG=DE,AG=AB=BC=CD=4,设FC=x,EC=y,则BF=4-x,DE=4-y,
∵BF+DE=FG+EG=EF=3,
∴4-x+4-y=3,
∴x+y=5 ①
在Rt![]() EFC中,∵EF2=EC2+FC2,
EFC中,∵EF2=EC2+FC2,
∴x2+y2=32 ②
①2-②得到,2xy=16,
∴S![]() CEF=
CEF=![]() xy=4.
xy=4.
【解析】(1)根据HL可得出△ABF![]() △ AGF;(2)只要证明
△ AGF;(2)只要证明![]() BAF=
BAF=![]() GAF,
GAF,![]() GAE=
GAE=![]() DAE,即可求出
DAE,即可求出![]() EAF=45
EAF=45![]() ;(3)设FC=x,EC=y,则BF=4-x,DE=4-y,构建方程组,求出xy即可求出△CEF的面积.
;(3)设FC=x,EC=y,则BF=4-x,DE=4-y,构建方程组,求出xy即可求出△CEF的面积.
【考点精析】掌握正方形的性质是解答本题的根本,需要知道正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AB是⊙O的直径,直线CP切⊙O于点C,过点B作BD⊥CP于D.
(1)求证:CB2=ABDB;
(2)若⊙O的半径为2,∠BCP=30°,求图中阴影部分的面积.
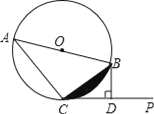
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题的个数是( )
①同位角相等
②经过一点有且只有一条直线与这条直线平行
③长度相等的弧是等弧
④顺次连接菱形各边中点得到的四边形是矩形.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.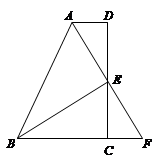
求证:
(1)AD=FC;
(2)AB=BC+AD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AC=5,BC=12,CO⊥AB于点O,D是线段OB上一点,DE=2,ED∥AC(∠ADE<90°),连接BE、CD.设BE、CD的中点分别为P、Q.
(1)求AO的长;
(2)求PQ的长;
(3)设PQ与AB的交点为M,请直接写出|PM﹣MQ|的值.
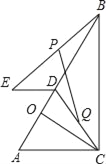
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列方程:①x﹣1=1;②x+y=2z;③2x﹣1<y;④3y﹣2=y2;⑤2x﹣y=0;⑥x﹣10>﹣5中一元一次方程的是( ),二元一次方程的是( ),一元一次不等式的是( )
A.①;⑤;⑥
B.④;⑤;⑥
C.④;②;③
D.①;②;③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com