
����Ŀ����ͼ��ֱ��y=��x+3�ֱ���x�ᡢy���ڵ�B��C��������y=x2+bx+c������B��C����x�����һ������Ϊ��A����A�ڵ�B����ࣩ���Գ���Ϊl1������ΪD��
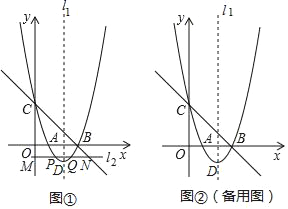
��1����������y=x2+bx+c�Ľ���ʽ��
��2����M��0��m��Ϊy����һ���㣬����M��ֱ��l2ƽ����x�ᣬ�������߽��ڵ�P��x1��y1����Q��x2��y2������ֱ��BC���ڵ�N��x3��y3������x2��x1��0��
�ٽ�Ϻ�����ͼ����x3��ȡֵ��Χ��
����������P��Q��N��ǡ����һ�����������������߶ε��е㣬��m��ֵ��
���𰸡���1��y=x2��4x+3����2����0��x3��4����m��ֵΪ![]() ��1��
��1��
��������
��1����ֱ��y=��x+3�ֱ���x�ᡢy���ڵ�B��C��õ�B��C�����꣬�ٴ���y=x2+bx+c���b��c��ֵ��������������ߵĽ���ʽ����2��������������ߵĶ�������ΪD��2����1������ֱ��l2������Dʱ���m=��1����ֱ��l2������Cʱ���m=3������x2��x1��0���ɵ���1��y3��3��������1����x3+3��3������0��x3��4���ڷֵ�ֱ��l2��x����·�ʱ����Q�ڵ�P��N֮��͵�ֱ��l2��x����Ϸ�ʱ����N�ڵ�P��Q֮�����������m��ֵ����.
��1����y=��x+3����x=0����y=3��
��y=0����x=3����B��3��0����C��0��3����
����B��3��0����C��0��3�����������y=x2+bx+c
�ã�![]() �����
����� ![]()
��y=x2��4x+3��
��2����ֱ��l2ƽ����x�ᣬ
��y1=y2=y3=m��
����ͼ����y=x2��4x+3=��x��2��2��1��
�ඥ��ΪD��2����1����
��ֱ��l2������Dʱ��m=��1��
��ֱ��l2������Cʱ��m=3
��x2��x1��0��
����1��y3��3��
����1����x3+3��3��
��0��x3��4��
����ͼ�٣���ֱ��l2��x����·�ʱ����Q�ڵ�P��N֮�䣬
��������P��Q��N��ǡ����һ�����������������߶ε��е㣬���PQ=QN��
��x2��x1��0��
��x3��x2=x2��x1��
�� x3=2x2��x1��
��l2��x�ᣬ��PQ��x�ᣬ
���P��Q���������ߵĶԳ���l1�Գƣ�
�������ߵĶԳ���l1Ϊx=2��
��2��x1=x2��2��
��x1=4��x2��
��x3=3x2��4��
����Q��x2��y2�����������y=x2��4x+3
��y2=x22��4x2+3����y2=y3=��x3+3
��x22��4x2+3=��x3+3��
��x22��4x2=����3x2��4��
�� x22��x2��4=0�����x2=![]() ������ֵ����ȥ����
������ֵ����ȥ����
��m=��![]() ��2��4��
��2��4��![]() +3=
+3=![]()
��ͼ�ڣ���ֱ��l2��x����Ϸ�ʱ����N�ڵ�P��Q֮�䣬
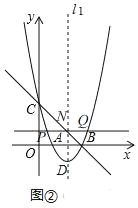
��������P��Q��N��ǡ����һ�����������������߶ε��е㣬���PN=NQ��
���Ͽɵõ�P��Q����ֱ��l1�Գƣ�
���N�������ߵĶԳ���l1��x=2��
�ֵ�N��ֱ��y=��x+3�ϣ�
��y3=��2+3=1����m=1��
��m��ֵΪ![]() ��1��
��1��


 ��ʦ�㾦�ִʾ��ƪϵ�д�
��ʦ�㾦�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ����ֱ��
����ֱ��![]() ���ڵ�
���ڵ�![]() ����
����![]() ��
��![]() ���ϵ�һ�����㣬��
���ϵ�һ�����㣬��![]() .
.
��1����![]() ��ֵ��С����
��ֵ��С����![]() ��ֵ��
��ֵ��
��2����ֱ��![]() ��
��![]() �ָ���������������Σ������
�ָ���������������Σ������![]() ��ֵ����˵������.
��ֵ����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С����һ����Ϸ�����Ŵ�С���ʵض���ͬ�Ŀ�Ƭ�Ϸֱ��������![]() ��
��![]() ��
��![]() ���ֽ��������ֵ�һ�泯�£�С����С�������������ȡһ�ţ�����С����С����õ���������֮�ͣ������Ϊ������С��ʤ����Ϊż����С��ʤ��
���ֽ��������ֵ�һ�泯�£�С����С�������������ȡһ�ţ�����С����С����õ���������֮�ͣ������Ϊ������С��ʤ����Ϊż����С��ʤ��
![]() ��С���鵽��������
��С���鵽��������![]() ��Ƭȡʤ�ĸ��ʣ�
��Ƭȡʤ�ĸ��ʣ�
![]() ���жϸ���Ϸ��˫���Ƿ�ƽ�������б�������״ͼ�ȷ���˵�����ɣ�
���жϸ���Ϸ��˫���Ƿ�ƽ�������б�������״ͼ�ȷ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��Ʒ�ı�־ͼ����AC��BD�ǡ�O������ֱ������β˳�����ӵ�A��B��C��D���õ��ı���ABCD����AC=10cm����BAC=36������ͼ����Ӱ���ֵ����Ϊ_____��
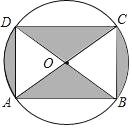
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳��ƻ�����һ���ס���������ߣ���֪һ��������ߵĽ�����һ��������ߵĽ��۵ĺ�Ϊ40Ԫ����90Ԫ����������ߵļ�������150Ԫ����������ߵļ�����ͬ��
��1����ÿ�����֡�������ߵĽ��۷ֱ��Ƕ���Ԫ��
��2���̳��ƻ������ס���������߹�48�������м�����ߵļ�������������ߵļ������̳������˴ν��������ʽ���1000Ԫ�����̳����м��ֽ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��![]() ��
��![]() ��
��![]() ���ϣ�
���ϣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ������������________�����ı���
������������________�����ı���![]() �Ǿ��Σ�����������________�����ı���
�Ǿ��Σ�����������________�����ı���![]() �����Σ�����������________�����ı���
�����Σ�����������________�����ı���![]() �������Σ�
��������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��Ӧ��ί����������Ľ��衰��ɫ�������ĺ��٣�����ij��λ����Ժ��һ�鳤30m����20m�ij����οյأ�����һ�����λ�.Ҫ���ڻ�������������ƽ�к�һ���������۵�С����ʣ��ĵط���ֲ���ݣ���ͼ��ʾ��Ҫʹ��ֲ���ݵ����Ϊ532m2����ôС�������ڵĿ���ӦΪ�����ף���ע������С�������ڵĿ�����ȣ���ÿ��С����Ϊƽ���ı��Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�γ�Ϊ40m�����Χ��һ��һ�߿�ǽ�ľ��λ���ABCD��ǽ��28m����AB��Ϊxm�����ε����Ϊym2��
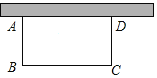
��1��д��y��x�ĺ�����ϵʽ��
��2����AB��Ϊ������ʱ����Χ�ɵĻ������������ֵ�Ƕ��٣�
��3�������Ե����Ϊ150m2ʱ��AB��Ϊ�����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��ƽ��ֱ������ϵ�У�������������![]() ��
��![]() ������
������![]() ����
����![]() ��
��![]() ����ô�Ƶ�
����ô�Ƶ�![]() �ǵ�
�ǵ�![]() ��
��![]() ���ںϵ�.
���ںϵ�.
���磺![]() ��
��![]() ������
������![]() ����
����![]() ��
��![]() ʱ�����
ʱ�����![]() �ǵ�
�ǵ�![]() ��
��![]() ���ںϵ㣬
���ںϵ㣬

��1����֪��![]() ��
��![]() ��
��![]() ����˵������һ������������������ںϵ�.
����˵������һ������������������ںϵ�.
��2����ͼ����![]() ����
����![]() ��ֱ��
��ֱ��![]() ������һ�㣬��
������һ�㣬��![]() �ǵ�
�ǵ�![]() ��
��![]() ���ںϵ�.
���ںϵ�.
����ȷ��![]() ��
��![]() �Ĺ�ϵʽ.
�Ĺ�ϵʽ.
����ֱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() Ϊֱ��������ʱ�����
Ϊֱ��������ʱ�����![]() ������.
������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com