Question

18．如图，抛物线Y=-$\frac{4}{9}$x²-$\frac{4}{9}$mx+$\frac{8}{9}$m²（m＞0）与x轴相交于A，B两点，点H是抛物线的顶点，以AB=6为直径作圆G交y轴于E，F两点，EF=4$\sqrt{2}$．
（1）求m的值；
（2）连结AH，求线段AH的长；
（3）点P是抛物线对称轴上的一点，且点P在x轴上方．若以P点为圆心的圆P与直线AH和x轴都相切，求点P的坐标．

Answer 1

分析 （1）根据函数解析式，求得方程x²+mx-2m²=0，的解为x₁=m，x₂=-2m，据此得到A（-2m，0），B（m，0），再根据AB=3m，AB=6，即可得到m=2；
（2）当m=2时，得到抛物线的顶点式：y=-$\frac{4}{9}$（x+1）²+4，得到H（-1，4），进而得出GH=4，再根据AG=$\frac{1}{2}$AB=3，根据勾股定理，得AH=$\sqrt{{3}^{2}+{4}^{2}}$=5；
（3）以P点为圆心的圆P与直线AH和x轴都相切时，过P作PM⊥AH于M，则PM=PG，AM=AG=3，MH=2，再设PM=PG=r，则PH=4-r，根据∠PMH=90°，得出Rt△HPM中，PM²+MH²=PH²，据此得到方程r²+2²=（4-r）²，求得r=$\frac{3}{2}$，再根据H（-1，4），点P是抛物线对称轴上的一点，即可得到P（-1，$\frac{3}{2}$）．

解答 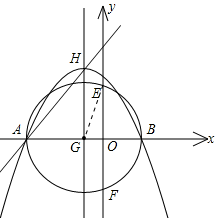解：（1）当y=0时，-$\frac{4}{9}$x²-$\frac{4}{9}$mx+$\frac{8}{9}$m²=0，
∴x²+mx-2m²=0，
解得x₁=m，x₂=-2m，
∴A（-2m，0），B（m，0），
∴AB=3m，
∵AB=6，
∴m=2；
解法二：
由抛物线y=-$\frac{4}{9}$x²-$\frac{4}{9}$mx+$\frac{8}{9}$m²可得，其对称轴为x=-$\frac{m}{2}$，
∴G（-$\frac{m}{2}$，0），
∵x轴⊥EF，AB是直径，EF=4$\sqrt{2}$，
∴EO=$\frac{1}{2}$EF=2$\sqrt{2}$．
连结GE，
∵Rt△EOG中，GE=3，
∴由勾股定理得${3^2}=（\frac{m}{2}{）^2}+（2\sqrt{2}{）^2}$，
解得m=±2，
∵m＞0，
∴m=2；

（2）当m=2时，y=-$\frac{4}{9}$x²-$\frac{8}{9}$x+$\frac{32}{9}$=-$\frac{4}{9}$（x+1）²+4，
∴H（-1，4），
∴GH=4，
∵AG=$\frac{1}{2}$AB=3，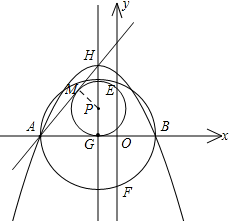
由勾股定理，得AH=$\sqrt{{3}^{2}+{4}^{2}}$=5；

（3）以P点为圆心的圆P与直线AH和x轴都相切时，
过P作PM⊥AH于M，则PM=PG，AM=AG=3，
∴MH=AH-AM=5-3=2，
设PM=PG=r，则PH=4-r，
∵∠PMH=90°，
∴Rt△HPM中，PM²+MH²=PH²，
即r²+2²=（4-r）²，
解得r=$\frac{3}{2}$，
∴PG=$\frac{3}{2}$，
又∵H（-1，4），点P是抛物线对称轴上的一点，
∴P（-1，$\frac{3}{2}$）．

点评 本题属于圆的综合题，主要考查了圆的性质，垂径定理，二次函数的图象与性质以及勾股定理的综合应用，解决问题的关键是作辅助线构造直角三角形，运用勾股定理列出一元二次方程，求得未知数的值．解题时注意方程思想的运用．