【题目】如图，平行四边形ABCD中，对角线AC，BD交于点O，且AC⊥BC，点E是BC延长线上一点， 
，连接DE.
(1)求证：四边形ACED为矩形；
(2)连接OE，如果BD=10，求OE的长.
【答案】(1)证明见解析；(2)OE=5.
【解析】
（1）由题干可知四边形ABCD是平行四边形，且
,可证明四边形ACED是平行四边形，又AC⊥BC，可证明四边形ACED是矩形；
（2）由（1）可得∠E=90°，在Rt△ADE中根据定理可得，OE=
BD，根据BD的长度可计算出OE的长度.
(1)证明：∵四边形ABCD是平行四边形，∴AD=BC，
，又∵ ，∴AD=CE∴四边形ABCD是平行四边形，又∵
，∴∠ACE=90°，∴四边形ACED是矩形.
(2)∵对角线AC，BD交于点O，∴点O是BD的中点，∵四边形ACED是矩形，∴∠E=90°，在Rt△ADE中根据定理可得OE=BD，又∵BD=10，∴ OE=5，故答案为5.
直通贵州名校周测月考直通名校系列答案
培优三好生系列答案科目：初中数学 来源： 题型：
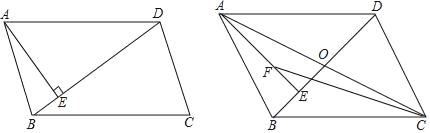
【题目】如图，在平行四边形ABCD中，AE⊥BD于E．
（1）若BC＝BD，
，AD＝15，求△ABD的周长．
（2）若∠DBC＝45°，对角线AC、BD交于点O，F为AE上一点，且AF＝2EO，求证：CF＝
AB．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商场试销一种成本为每件
元的服装，规定试销期间销售单价不低于成本单价，且获利不得高于
，经试销发现，销售量
（件）与销售单价
（元）符合一次函数
，且
时，
；
时，
．
求一次函数的表达式；
若该商场获得利润为
元，试写出利润与销售单价之间的关系式；销售单价定为多少元时，商场可获得最大利润，最大利润是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，利用一面长为34米的墙，用铁栅栏围成一个矩形自行车场地ABCD，在AB和BC边各有一个2米宽的小门（不用铁栅栏）．设矩形ABCD的边AD长为x米，AB长为y米，矩形的面积为S平方米，且x＜y．
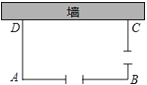
（1）若所用铁栅栏的长为40米，求y与x的函数关系式，并直接写出自变量x的取值范围；
（2）在（1）的条件下，求S与x的函数关系式，并求出怎样围才能使矩形场地的面积为192平方米？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD的对角线相交于点O，点E，F分别是边BC上两点，且
.将
绕点O逆时针旋转，当点F与点C重合时，停止旋转.已知，BC=6，设BE=x，EF=y.
小明根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究.
下面是小明的探究过程，请补充完整：
(1)按照下表中自变量x的值进行取点、画图、测量，得到了y与x的几组对应值；
x | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 |
y | 3 | 2.77 | 2.50 | 2.55 | 2.65 |
(说明：补全表格时相关数值保留一位小数)
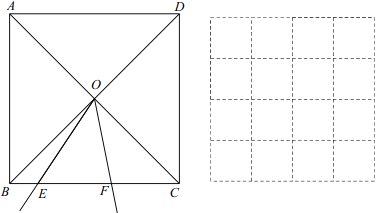
(2)建立平面直角坐标系，描出补全后的表中各对对应值为坐标的点，画出该函数的图象；
(3)结合函数图象，解决问题：当EF=2BE时，BE的长度约为______.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线AB、CD相交于点O，∠AOC=30°，半径为2cm的P的圆心在射线OA上，且与点O的距离为6cm，如果P以1cm/s的速度沿直线AB由A向B的方向移动，那么P与直线CD相切时☉P运动的时间是（ ）
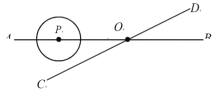
A.3秒或10秒B.3秒或8秒C.2秒或8秒D.2秒或10秒
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】口袋中有
只乒乓球，其中
只是红球，另
只是黄球，它们的大小都一样，现从中任意摸出只球，
（1）恰为一红一黄的概率是多少？
（2）两只均为红球的概率是多少？
（3）两只均为黄球的概率是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
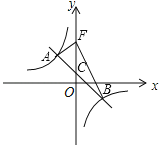
【题目】在平面直角坐标系中，一次函数y＝﹣x+b的图象与反比例函数y＝
(k≠0)的图象交于A、B点，与y轴交于点C，其中点A的半标为(﹣2，3)
(1)求一次函数和反比例函数的解析式；
(2)如图，若将点C沿y轴向上平移4个单位长度至点F，连接AF、BF，求△ABF的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
