
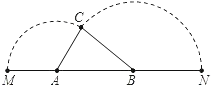
【题目】已知A、B是线段MN上的两点,MN=4,MA=1,MB>1.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC.设AB=x,请解答:(1)x的取值范围______;
(2)若△ABC是直角三角形,则x的值是______.
【答案】1<x<2 x![]() 或x
或x![]() .
.
【解析】
(1)因为所求AB或x在△ABC中,所以可利用三角形三边之间的关系即两边之和大于第三边,两边之差小于第三边进行解答.
(2)应该分情况讨论,因为不知道在三角形中哪一个是作为斜边存在的.所以有三种情况,即:①若AC为斜边,则1=x2+(3-x)2,即x2-3x+4=0,无解;②若AB为斜边,则x2=(3﹣x)2+1,解得x![]() ,满足1<x<2;③若BC为斜边,则(3﹣x)2=1+x2,解得:x
,满足1<x<2;③若BC为斜边,则(3﹣x)2=1+x2,解得:x![]() ,满足1<x<2;
,满足1<x<2;
解:
(1)∵MN=4,MA=1,AB=x,
∴BN=4﹣1﹣x=3﹣x,
由旋转的性质得:MA=AC=1,BN=BC=3﹣x,
由三角形的三边关系得
![]() ,
,
∴x的取值范围是1<x<2.
故答案为:1<x<2;
(2)∵△ABC是直角三角形,
∴若AC为斜边,则1=x2+(3﹣x)2,即x2﹣3x+4=0,无解,
若AB为斜边,则x2=(3﹣x)2+1,解得:x![]() ,满足1<x<2,
,满足1<x<2,
若BC为斜边,则(3﹣x)2=1+x2,解得:x![]() ,满足1<x<2,
,满足1<x<2,
故x的值为:x![]() 或x
或x![]() .
.
故答案为:x![]() 或x
或x![]() .
.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】某校检测学生跳绳水平,抽样调查了部分学生的“1分钟跳绳”成绩,并制成了下面的频数分布直方图(每小组含最小值,不含最大值)和扇形图

(1)D组的人数是 人,补全频数分布直方图,扇形图中m= ;
(2)本次调查数据中的中位数落在 组;
(3)如果“1分钟跳绳”成绩大于或等于120次为优秀,那么该校4500名学生中“1分钟跳绳”成绩为优秀的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,黔南州近期举办了中小学生“国学经典大赛”.比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式分“单人组”和“双人组”.
(1)小丽参加“单人组”,她从中随机抽取一个比赛项目,恰好抽中“三字经”的概率是多少?
(2)小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少?请用画树状图或列表的方法进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .动点
.动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 向终点
向终点![]() 以
以![]() /
/![]() 的速度运动,同时动点
的速度运动,同时动点![]() 从点
从点![]() 出发,沿折线
出发,沿折线![]() 以
以![]() /
/![]() 的速度向终点
的速度向终点![]() 运动,当有一点到达终点时,另一点也停止运动,以
运动,当有一点到达终点时,另一点也停止运动,以![]() 、
、![]() 为邻边作设
为邻边作设![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]()
![]() 点
点![]() 运动的时间为
运动的时间为![]() .
.
(1)当点![]() 在
在![]() 边上时,求
边上时,求![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(2)当点![]() 落在线段
落在线段![]() 上时,求
上时,求![]() 的值;
的值;
(3)求![]() 与
与![]() 之间的函数关系式
之间的函数关系式![]() ,并写出自变量
,并写出自变量![]() 的取值范围.
的取值范围.
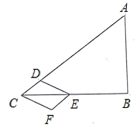
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在Rt△ABC中,∠C=90°,BD平分∠ABC,过D作DE⊥BD交AB于点E,经过B,D,E三点作⊙O.
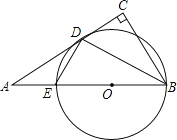
(1)求证:AC与⊙O相切于D点;
(2)若AD=15,AE=9,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件
(1)写出商场销售这种文具,每天所得的销售利润![]() (元)与销售单价
(元)与销售单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元
请比较哪种方案的最大利润更高,并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用一面长为34米的墙,用铁栅栏围成一个矩形自行车场地ABCD,在AB和BC边各有一个2米宽的小门(不用铁栅栏)设矩形ABCD的边AD长为x米,AB长为y米,矩形的面积为S平方米,且x<y.
(1)若所用铁栅栏的长为40米,写出y与x的函数关系式,并求出自变量x的取值范围:
(2)在(1)的条件下,求S与x的函数关系式,并求出怎样围才能使矩形场地的面积为192平方米?
(3)在(2)的条件下,请直接写出当矩形场地的面积大于192平方米时x的取值范围.
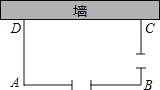
查看答案和解析>>
科目:初中数学 来源: 题型:
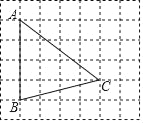
【题目】如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上.
(Ⅰ)AC的长等于_____;
(Ⅱ)在线段AC上有一点D,满足AB2=ADAC,请在如图所示的网格中,用无刻度的直尺,画出点D,并简要说明点D的位置是如何找到的(不要求证明)_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程![]() .
.
(1)求证:无论k取什么实数值,这个方程总有实数根;
(2)当![]() =3时,△ABC的每条边长恰好都是方程
=3时,△ABC的每条边长恰好都是方程![]() 的根,求△ABC的周长.
的根,求△ABC的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com