
【题目】如图在Rt△ABC中,∠C=90°,BD平分∠ABC,过D作DE⊥BD交AB于点E,经过B,D,E三点作⊙O.
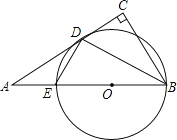
(1)求证:AC与⊙O相切于D点;
(2)若AD=15,AE=9,求⊙O的半径.
【答案】(1)见解析;(2)8.
【解析】
试题分析:(1)连接OD,则有∠1=∠2,而∠2=∠3,得到∠1=∠3,因此OD∥BC,又由于∠C=90°,所以OD⊥AD,即可得出结论.
(2)根据OD⊥AD,则在RT△OAD中,OA2=OD2+AD2,设半径为r,AD=15,AE=9,得到(r+9)2=152+r2,解方程即可.
(1)证明:连接OD,如图所示:
∵OD=OB,
∴∠1=∠2,
又∵BD平分∠ABC,
∴∠2=∠3,
∴∠1=∠3,
∴OD∥BC,
而∠C=90°,
∴OD⊥AD,
∴AC与⊙O相切于D点;
(2)解:∵OD⊥AD,
∴在RT△OAD中,OA2=OD2+AD2,
又∵AD=15,AE=9,设半径为r,
∴(r+9)2=152+r2,
解方程得,r=8,
即⊙O的半径为8.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】跳跳一家外出自驾游,出发时油箱里还剩有汽油30升,已知跳跳家的汽车每百千米的平均油耗为12升,设油箱里剩下的油量为y(单位:升),汽车行驶的路程为x(单位:千米).
(1)求y关于x的函数表达式;
(2)若跳跳家的汽车油箱中的油量低于5升时,仪表盘会亮起黄灯警报. 要使邮箱中的存油量不低于5升,跳跳爸爸至多能够行驶多少千米就要进加油站加油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市大力发展乡村旅游产业,全力打造客都美丽乡村”,其中“客家美景、客家文化、客家美食”享誉全省,游人络绎不绝.去年我市某村村民抓住机遇,投入20万元创办农家乐(餐饮+住宿),一年时间就收回投资的80%,其中餐饮收入是住宿收入的2倍还多1万元.
(1)求去年该农家乐餐饮和住宿的收入各为多少万元?
(2)今年该村村民再投入了10万元,增设了土特产的实体销售和网上销售项目并实现盈利,村民在接受记者采访时说,预计今年餐饮和住宿的收入比去年还会有10%的增长.这两年的总收入除去所有投资外还能获得不少于10万元的纯利润,请问今年土特产销售至少收入多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B是线段MN上的两点,MN=4,MA=1,MB>1.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC.设AB=x,请解答:(1)x的取值范围______;
(2)若△ABC是直角三角形,则x的值是______.
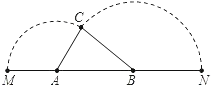
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:① abc>0;② 2a+b=0;③ 当m≠1时,a+b>am2+bm;④ a-b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,x1+x2=2,
其中正确的有( )
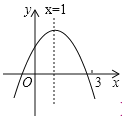
A. ①②③ B. ②④ C. ②⑤ D. ②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则图中阴影部分的面积是( )
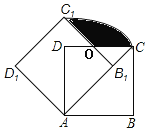
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数![]() (x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.
(x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.
(1)求△OCD的面积;
(2)当BE=![]() AC时,求CE的长.
AC时,求CE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com