
【题目】如图①,在矩形 ABCD中,AB=10cm,BC=8cm.点P从A出发,沿A→B→C→D路线运动,到D停止;点Q从D出发,沿 D→C→B→A路线运动,到A停止.若点P、点Q同时出发,点P的速度为每秒1cm,点Q的速度为每秒2cm,a秒时点P、点Q同时改变速度,点P的速度变为每秒bcm,点Q的速度变为每秒dcm.图②是点P出发x秒后△APD的面积S1(cm2)与x(秒)的函数关系图象;图③是点Q出发x秒后△AQD的面积S2(cm2)与x(秒)的函数关系图象.
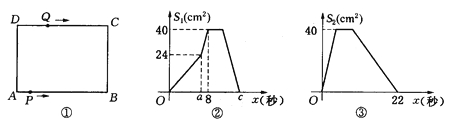
(1)、参照图象,求b、图②中c及d的值;
(2)、连接PQ,当PQ平分矩形ABCD的面积时,运动时间x的值为 ;
(3)、当两点改变速度后,设点P、Q在运动线路上相距的路程为y(cm),求y(cm)与运动时间x(秒)之间的函数关系式,并写出自变量x的取值范围;
(4)、若点P、点Q在运动路线上相距的路程为25cm,求x的值.
【答案】(1)、b=2;C=17;d=1;(2)、![]() ;(3)、当6<x≤
;(3)、当6<x≤![]() 时,y=28-3x;当
时,y=28-3x;当![]() <x≤17时,y=3x-28; 当17<x≤22时,y=x+6;(4)、1秒或19秒.
<x≤17时,y=3x-28; 当17<x≤22时,y=x+6;(4)、1秒或19秒.
【解析】
试题分析:(1)、首先根三角形面积求出a的值,然后得出b、c、d的值;(2)、平分面积则说明PQ经过四边形对角线的交点,然后根据题意得出答案;(3)、利用待定系数法求出一次函数的解析式;(4)、本题分改变速度之前和改变速度之后两种情况分别求出x的值.
试题解析:(1)、观察图②得S△APD=![]() PAAD=
PAAD=![]() ×a×8=24, ∴a=6(秒),
×a×8=24, ∴a=6(秒),
![]() (厘米/秒),
(厘米/秒), ![]() (秒);
(秒);
(22﹣6)d=28﹣12, 解得d=1(厘米/秒);
(2)、![]()
(3)、当6<x≤![]() 时,y=28-3x 当
时,y=28-3x 当![]() <x≤17时,y=3x-28 当17<x≤22时,y=x+6
<x≤17时,y=3x-28 当17<x≤22时,y=x+6
(4)、改变速度前,28-3x=25,x=1 改变速度后,x+6=25,x=19
∴当点Q出发1或19秒时,点P、点Q在运动路线上相距的路程为25cm.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,顶点为(4,1)的抛物线交y轴于点A,交x轴于B,C两点(点B在点C的左侧),已知C点坐标为(6,0).

(1)求此抛物线的解析式;
(2)已知点P是抛物线上的一个动点,且位于A,C两点之间.问:当点P运动到什么位置时,△PAC的面积最大?求出△PAC的最大面积;
(3)连接AB,过点B作AB的垂线交抛物线于点D,以点C为圆心的圆与抛物线的对称轴l相切,先补全图形,再判断直线BD与⊙C的位置关系并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=30°,沿BE将此三角形对折,又沿BA′再一次对折,点C落在BE上的C′处,此时∠C′DB=84°,则原三角形的∠ABC的度数为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D为BC边的中点,以点D为顶点的∠EDF的两边分别与边AB,AC交于点E,F,且∠EDF与∠A互补.
(1)如图1,若AB=AC,且∠A=90°,则线段DE与DF有何数量关系?请直接写出结论;
(2)如图2,若AB=AC,那么(1)中的结论是否还成立?若成立,请给出证明;若不成立,请说明理由;
(3)如图3,若AB:AC=m:n,探索线段DE与DF的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列合并同类项正确的有( ).
①-2mn+2nm=0;
②3x2+22x2=5x2;
③x2+2x2-5x2=-2x2;
④(-y)2+y2=0.
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中装有4个红球和若干个白球,它们除颜色外其他完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有____个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.
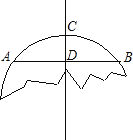
①求作此残片所在的圆O(不写作法,保留作图痕迹);
②已知:AB=12cm,直径为20cm,求①中CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com