
����Ŀ����ͼ������ABC�У���DΪBC�ߵ��е㣬�Ե�DΪ�������EDF�����߷ֱ����AB��AC���ڵ�E��F������EDF����A������
��1����ͼ1����AB=AC������A=90�������߶�DE��DF�к�������ϵ����ֱ��д�����ۣ�
��2����ͼ2����AB=AC����ô��1���еĽ����Ƿ������������������֤����������������˵�����ɣ�
��3����ͼ3����AB��AC=m��n��̽���߶�DE��DF��������ϵ����֤����Ľ��ۣ�

���𰸡���1��DE=DF����2��DE=DF��Ȼ����������������3��������
��������
�����������1�����ȸ��ݵ��������ε����ʿɵ���DAB=��DAC=![]() ��BAC��AD��BC����֤����C=��B=45������ADE=��FDC��AD=DC��������ASA����֤����AED�ա�CFD�������õ�DE=DF��
��BAC��AD��BC����֤����C=��B=45������ADE=��FDC��AD=DC��������ASA����֤����AED�ա�CFD�������õ�DE=DF��
��2��DE=DF��Ȼ��������ͼ2������D��DM��AB��M����DN��AC��N������AD������EMD=��FND=90��������AB=AC����DΪBC�е㣬���������ε��������ߺ�һ�õ�ADƽ����BAC�����ǵõ�DM=DN�����ı���AMDN�У�����DMA=��DNA=90�����õ���MAN+��MDN=180������������EDF����MAN������֤����MDN=��EDF���Ƴ���DEM�ա�DFN��ASA�������ɵõ����ۣ�
��3������DE��DF=n��m����ͼ3������D��DM��AB��M����DN��AC��N������ADͬ��2����֤��1=��2��ͨ����DEM�ס�DFN���õ�![]() �����ڵ�EΪAC���е㣬�õ�S��ABD=S��ADC���еȻ�ʽ���ɵõ����ۣ�
�����ڵ�EΪAC���е㣬�õ�S��ABD=S��ADC���еȻ�ʽ���ɵõ����ۣ�
�⣺��1��DF=DE��
���ɣ���ͼ1������AD��
��Rt��ABC�ǵ��������Σ�
���C=��B=45����
��D��б��BC���е㣬
���DAB=��DAC=![]() ��BAC=45����AD��BC��
��BAC=45����AD��BC��
��AD=DC��
�ߡ�EDF=90����
���ADF+��ADE=90����
��AD��BC��
���ADC=90����
���ADF+��FDC=90����
���ADE=��FDC��
����ADE����CDF�� ��
��
���AED�ա�CFD��ASA����
��DE=DF��
��2��DE=DF��Ȼ������
��ͼ2������D��DM��AB��M����DN��AC��N������AD��
����EMD=��FND=90�㣬
��AB=AC����DΪBC�е㣬
��ADƽ����BAC��
��DM=DN��
�����ı���AMDN�У�����DMA=��DNA=90����
���MAN+��MDN=180����
���ߡ�EDF����MAN������
���MDN=��EDF��
���1=��2������DEM����DFN�� ��
��
���DEM�ա�DFN��ASA����
��DE=DF��
��3������DE��DF=n��m��
��ͼ3������D��DM��AB��M����DN��AC��N������AD��
ͬ��2����֤��1=��2��
���ߡ�EMD=��FND=90����
���DEM�ס�DFN��
��![]() ��
��
����DΪBC�ߵ��е㣬
��S��ABD=S��ADC��
��![]() ��
��
��![]() ��
��
����![]() ��
��
��![]() ��
��






| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ�ĸ�����(����)��
(1)�����������ĺͱ�����������
(2)�����������Ļ�������������
(3)��������������������0������������
(4)ʵ���������ϵĵ���һһ��Ӧ�ģ�
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУͼ���ȥ�����ͼ��5��ᣬԤ�Ƶ�����������ӵ�7.2��ᣬ�����������ƽ��������Ϊ___________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ھ��� ABCD�У�AB��10cm��BC��8cm����P��A��������A��B��C��D·���˶�����Dֹͣ����Q��D�������� D��C��B��A·���˶�����Aֹͣ������P����Qͬʱ��������P���ٶ�Ϊÿ��1cm����Q���ٶ�Ϊÿ��2cm��a��ʱ��P����Qͬʱ�ı��ٶȣ���P���ٶȱ�Ϊÿ��bcm����Q���ٶȱ�Ϊÿ��dcm��ͼ���ǵ�P����x�����APD�����S1��cm2����x���룩�ĺ�����ϵͼ��ͼ���ǵ�Q����x�����AQD�����S2��cm2����x���룩�ĺ�����ϵͼ��
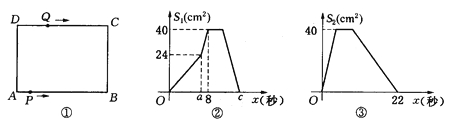
(1)������ͼ����b��ͼ����c��d��ֵ��
(2)������PQ����PQƽ�־���ABCD�����ʱ���˶�ʱ��x��ֵΪ ��
(3)��������ı��ٶȺ����P��Q���˶���·������·��Ϊy��cm������y��cm�����˶�ʱ��x���룩֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
(4)������P����Q���˶�·��������·��Ϊ25cm����x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʵ�ʾ�����500 m������ͼ�ϵľ�����25 cm�����ڴ�ͼ������A��B�������Ϊ40 cm����A��B���ص�ʵ�ʾ����ǣ� ��
A. 800 m B. 8000 m C. 32250 cm D. 3225 m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ı���ABCD��ƽ���ı��Σ����н����в���ȷ���ǣ� ��
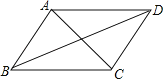
A����AB=BCʱ����������
B����AC��BDʱ����������
C������ABC=90��ʱ�����Ǿ���
D����AC=BDʱ������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ���ı���ABCD�У�E��F�ֱ�Ϊ��AB��CD���е㣬����DE��BF��BD��
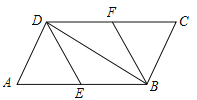
��1����֤����ADE�ա�CBF��
��2����AD��BD�����ı���BFDE��ʲô�����ı��Σ���֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪D����ABC��һ��BC�ϵ��е� ��AC��BE������ED���ӳ�ED��AC�ڵ�N����DM��EN�ڵ�D��AB�ڵ�M.
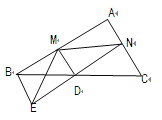
��1����֤��BE=CN
��2�����ж�BM+CN��MN�Ĵ�С��ϵ����˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com