
【题目】在平行四边形ABCD中,E,F分别为边AB,CD的中点,连接DE,BF,BD.
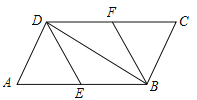
(1)求证:△ADE≌△CBF.
(2)若AD⊥BD,则四边形BFDE是什么特殊四边形?请证明你的结论.
【答案】(1)、证明过程见解析;(2)、菱形;证明过程见解析.
【解析】
试题分析:(1)、根据平行四边形的性质得到AD=BC,AB=CD,∠A=∠C,根据中点得到AE=CF,从而说明三角形全等;(2)、首先判断BFDE为平行四边形,根据直角三角形斜边上的中线的性质得到DE=BE,从而说明四边形BFDE为菱形.
试题解析:(1)、∵四边形ABCD为平行四边形 ∴AD=BC AB=CD ∠A=∠C
∵E,F分别为AB,CD的中点 ∴AE=CF ∴△ADE≌△CBF
、∵ABCD为平行四边形,E,F分别为AB,CD的中点 ∴DF=BE DF∥BE
∴四边形BFDE为平行四边形 ∵AD⊥BD ∴△ABD为直角三角形 DE为三角形斜边上的中线
∴DE=BE ∴四边形BFDE为菱形.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “任意画一个三角形,其内角和为360°”是随机事件;
B. 已知某篮球运动员投篮投中的概率为0.6,则他投十次可投中6次;
C. 抽样调查选取样本时,所选样本可按自己的喜好选取;
D. 检测某城市的空气质量,采用抽样调查法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D为BC边的中点,以点D为顶点的∠EDF的两边分别与边AB,AC交于点E,F,且∠EDF与∠A互补.
(1)如图1,若AB=AC,且∠A=90°,则线段DE与DF有何数量关系?请直接写出结论;
(2)如图2,若AB=AC,那么(1)中的结论是否还成立?若成立,请给出证明;若不成立,请说明理由;
(3)如图3,若AB:AC=m:n,探索线段DE与DF的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中装有4个红球和若干个白球,它们除颜色外其他完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有____个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某校九年级安全疏散演习中,各班疏散的时间分别是3分,2分40秒,3分20秒,3分30秒,2分45秒,这次演习中,疏散时间的极差为____秒.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E.∠ADC =70°.

(1)求∠EDC的度数;
(2)若∠ABC =n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移, 使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示),不改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBFE是菱形?为什么?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com