
【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E.∠ADC =70°.

(1)求∠EDC的度数;
(2)若∠ABC =n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移, 使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示),不改变,请说明理由.
【答案】(1)、35°;(2)、(![]() n+35)°;(3)、(215-
n+35)°;(3)、(215-![]() n)°.
n)°.
【解析】
试题分析:(1)、根据角平分线直接得出答案;(2)、过点E作EF∥AB,然后根据平行线的性质和角平分线的性质求出角度;(3)、首先根据题意画出图形,然后过点E作EF∥AB,按照第二小题同样的方法进行计算角度.
试题解析:(1)、∵DE平分∠ADC,∠ADC=70°,
∴∠EDC=![]() ∠ADC=
∠ADC=![]() ×70°=35°;
×70°=35°;
(2)、过点E作EF∥AB,
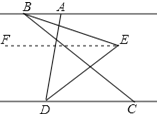
∵AB∥CD,
∴AB∥CD∥EF,
∴∠ABE=∠BEF,∠CDE=∠DEF,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°,
∴∠ABE=![]() ∠ABC=
∠ABC=![]() n°,∠CDE=
n°,∠CDE=![]() ∠ADC=35°,
∠ADC=35°,
∴∠BED=∠BEF+∠DEF=![]() n°+35°;
n°+35°;
(3)、过点E作EF∥AB
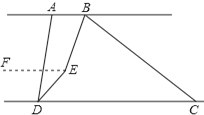
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°
∴∠ABE=![]() ∠ABC=
∠ABC=![]() n°,∠CDE=
n°,∠CDE=![]() ∠ADC=35°
∠ADC=35°
∵AB∥CD,
∴AB∥CD∥EF,
∴∠BEF=180°-∠ABE=180°-![]() n°,∠CDE=∠DEF=35°,
n°,∠CDE=∠DEF=35°,
∴∠BED=∠BEF+∠DEF=180°-![]() n°+35°=215°-
n°+35°=215°-![]() n°.
n°.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,E,F分别为边AB,CD的中点,连接DE,BF,BD.
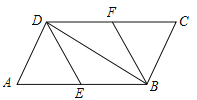
(1)求证:△ADE≌△CBF.
(2)若AD⊥BD,则四边形BFDE是什么特殊四边形?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中, A、B两点分别在x轴、y轴的正半轴上,且OB = OA=3.

(1)、求点A、B的坐标;
(2)、已知点C(-2,2),求△BOC的面积;
(3)、点P是第一象限角平分线上一点,若![]() ,求点P的坐标.
,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
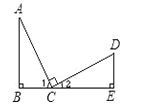
A. ∠1=∠2 B. ∠A =∠2 C. △ABC≌△CED D. ∠A与∠D互为余角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知D是△ABC中一边BC上的中点 ,AC∥BE,连接ED并延长ED交AC于点N,作DM⊥EN于点D交AB于点M.
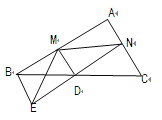
(1)求证:BE=CN
(2)试判断BM+CN与MN的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中正确的是( )
A. 有一组邻边相等的四边形是菱形 B. 有一个角是直角的平行四边形是矩形
C. 对角线垂直的平行四边形是正方形 D. 一组对边平行的四边形是平行四边形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com