
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����Ϊ��4��1���������߽�y���ڵ�A����x����B��C���㣨��B�ڵ�C����ࣩ����֪C������Ϊ��6��0����

��1����������ߵĽ���ʽ��
��2����֪��P���������ϵ�һ�����㣬��λ��A��C����֮�䣮�ʣ�����P�˶���ʲôλ��ʱ����PAC�������������PAC����������
��3������AB������B��AB�Ĵ��߽��������ڵ�D���Ե�CΪԲ�ĵ�Բ�������ߵĶԳ���l���У��Ȳ�ȫͼ�Σ����ж�ֱ��BD����C��λ�ù�ϵ������֤����
���𰸡���1��y=��![]() x2+2x��3����2��P���λ���ǣ�3��
x2+2x��3����2��P���λ���ǣ�3��![]() ������PAC����������
������PAC����������![]() ����3��P���λ���ǣ�3��
����3��P���λ���ǣ�3��![]() ������PAC����������
������PAC����������![]() ��
��
��������
�����������1���������߶���Ϊ��4��1����������䶥��ʽy=a��x��4��2+1����C�㣨6��0���������м������a��ֵ��
��2�����P�����꣨m����![]() m2+2m��3�����ú�m�Ķ���ʽ����ʾ����PAC��������ݽ⼫ֵ���⼴�ɵó���PAC�����ȡ���ֵʱP������꣬�Լ�������ֵ��
m2+2m��3�����ú�m�Ķ���ʽ����ʾ����PAC��������ݽ⼫ֵ���⼴�ɵó���PAC�����ȡ���ֵʱP������꣬�Լ�������ֵ��
��3����ͼ���ø����ߣ����������������εı�����ϵ���C��ֱ��BD�ľ��룬������C�뾶���бȽϣ����ɵó����ۣ�
��1���⣺�������ߵĶ���Ϊ��4��1����
���������߽���ʽΪy=a��x��4��2+1��
�������߾�����C��6��0����
��0=a��6��4��2+1�����a=��![]() ��
��
��y=��![]() ��x��4��2+1=��
��x��4��2+1=��![]() x2+2x��3��
x2+2x��3��
���������ߵĽ���ʽΪy=��![]() x2+2x��3��
x2+2x��3��
��2���⣺��ͼ1������P��ƽ����y���ֱ�߽�AC�ڵ�Q��
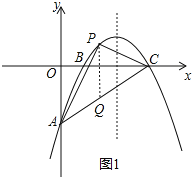
��A��0����3����C��6��0����
��ֱ��AC����ʽΪy=![]() x��3��
x��3��
��P��������m����![]() m2+2m��3����
m2+2m��3����
��Q���������m��![]() m��3����
m��3����
��PQ=��![]() m2+2m��3����
m2+2m��3����![]() m��3��=��
m��3��=��![]() m2+
m2+![]() m��
m��
��S��PAC=S��PAQ+S��PCQ=![]() ������
������![]() m2+
m2+![]() m����6=��
m����6=��![]() ��m��3��2+
��m��3��2+![]() ��
��
����m=3ʱ����PAC��������Ϊ![]() ��
��
����m=3ʱ����![]() m2+2m��3=
m2+2m��3=![]() ��
��
��P��������3��![]() ����
����
���ϣ�P���λ���ǣ�3��![]() ������PAC����������
������PAC����������![]() ��
��
��3���ж�ֱ��BD����C���룮
֤�����![]() ��x��4��2+1=0�����x1=2��x2=6��
��x��4��2+1=0�����x1=2��x2=6��
��B�����꣨2��0����
���������߽�y���ڵ�A��
��A��������0����3����
��AB=![]() =
=![]() ��
��
����C��Գ���l�����ڵ�F������C�İ뾶CF=2��
��CE��BD�ڵ�E����ͼ2������BEC=��AOB=90����
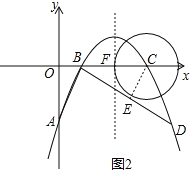
�ߡ�ABD=90����
���CBE=90������ABO��
���ߡ�BAO=90������ABO��
���BAO=��CBE��
���AOB�ס�BEC��
��![]() =
=![]() ��
��
��![]() =
=![]() ��
��
��CE=![]() ��2��
��2��
��ֱ��BD����C���룮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������1��2��3��a��ƽ������3������4��5��a��b��������5����a+b=____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ȱ�װ���˷���Դ����Ⱦ�������ݲ��㣬���ȫ��ÿ�����ʮ��֮һ�İ�װֽ��������ô�ܼ���3120000�ֶ�����̼���ŷ�����������3120000�ÿ�ѧ��������ʾΪ��������
A. 312��104 B. 0.312��107 C. 3.12��106 D. 3.12��107
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�꼶��֯ѧ���μ�����Ӫ�����������Ӫ��Ϊ�ס��ҡ���������л����������ͳ��ͼ��ӳ��ѧ�������μ�����Ӫ��������������ͼ�е���Ϣ�ش��������⣺
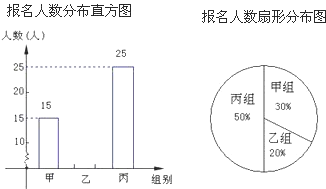
��1�����꼶�����μӱ��������Ϊ ��
��2�����꼶�����μӱ��λ�������� ������ȫƵ���ֲ�ֱ��ͼ��
��3������ʵ���������Ӽ���������ͬѧ�����飬ʹ���������Ǽ���������3����Ӧ�Ӽ�����������ѧ�������飿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������Ϊ�˽�ȫ�а��꼶ѧ������ѧ֪ʶ�������������һ����ѧ����У���ȫ��24000�����꼶�����������ȡ����ѧ������ѧ�ɼ����е��飬�������������Ƴ�����ͼ����

���������ͼ���ṩ����Ϣ������������⣺
��1������![]() ��
��![]() ����ʾ�����ֱ�Ϊ��
����ʾ�����ֱ�Ϊ��![]() = ��
= ��![]() = ��
= ��
��2������ͼ�У���ȫƵ���ֲ�ֱ��ͼ��
��3������ѳɼ���90�����ϣ���90�֣���Ϊ���㣬��ô����24000�����꼶������ѧ�ɼ�Ϊ�����ѧ��Լ�ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ھ��� ABCD�У�AB��10cm��BC��8cm����P��A��������A��B��C��D·���˶�����Dֹͣ����Q��D�������� D��C��B��A·���˶�����Aֹͣ������P����Qͬʱ��������P���ٶ�Ϊÿ��1cm����Q���ٶ�Ϊÿ��2cm��a��ʱ��P����Qͬʱ�ı��ٶȣ���P���ٶȱ�Ϊÿ��bcm����Q���ٶȱ�Ϊÿ��dcm��ͼ���ǵ�P����x�����APD�����S1��cm2����x���룩�ĺ�����ϵͼ��ͼ���ǵ�Q����x�����AQD�����S2��cm2����x���룩�ĺ�����ϵͼ��
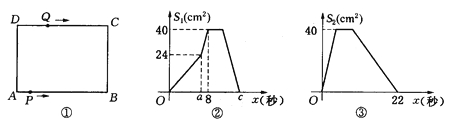
(1)������ͼ����b��ͼ����c��d��ֵ��
(2)������PQ����PQƽ�־���ABCD�����ʱ���˶�ʱ��x��ֵΪ ��
(3)��������ı��ٶȺ����P��Q���˶���·������·��Ϊy��cm������y��cm�����˶�ʱ��x���룩֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
(4)������P����Q���˶�·��������·��Ϊ25cm����x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У��߳�Ϊ3��������OABC��������A��C�ֱ���y�ᡢx����������ϣ���O��ԭ�㣮�ֽ�������OABC��O��˳ʱ����ת����A���һ������ֱ��y=x��ʱֹͣ��ת����ת�����У�AB�߽�ֱ��y=x�ڵ�M��BC�߽�x���ڵ�N����ͼ��������ת������OABC�Ĺ����У���MBN���ܳ�Ϊ ��
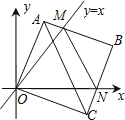
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com