
ЁОЬтФПЁПдФЖСНтЬтЙ§ГЬ,ЛиД№ЮЪЬт.
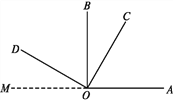
ШчЭМ,OCдкЁЯAOBФк,ЁЯAOBКЭЁЯCODЖМЪЧжБНЧ,ЧвЁЯBOC=30Ёу,ЧѓЁЯAODЕФЖШЪ§.
Нт:Й§OЕузїЩфЯпOM,ЪЙЕуM,O,AдкЭЌвЛжБЯпЩЯ.
вђЮЊЁЯMOD+ЁЯBOD=90Ёу,ЁЯBOC+ЁЯBOD=90Ёу,ЫљвдЁЯBOC=ЁЯMOD,
ЫљвдЁЯAOD=180Ёу-ЁЯBOC=180Ёу-30Ёу=150Ёу.
(1)ШчЙћЁЯBOC=60Ёу,ФЧУДЁЯAODЕШгкЖрЩйЖШ?ШчЙћЁЯBOC=nЁу,ФЧУДЁЯAODЕШгкЖрЩйЖШ?
(2)ШчЙћЁЯAOB=ЁЯDOC=xЁу,ЁЯAOD=yЁу,ЧѓЁЯBOCЕФЖШЪ§.
ЁОД№АИЁПЃЈ1ЃЉ120ЁуЃЌ180Ёу-nЁуЃЛЃЈ2ЃЉ2xЁу-yЁу.
ЁОНтЮіЁПЪдЬтЗжЮі:(1)ИљОнНЧЕФКЭВюЙиЯЕНјааМЦЫуПЩЧѓЕУ:
ШчЙћЁЯBOC=60ЁуЪБ,
ЁЯAOD=ЁЯCOD+ЁЯAOC=ЁЯCOD+(90ЁуЃЁЯCOB)= 90Ёу+(90ЁуЃ60Ёу)= 90Ёу+30Ёу=120Ёу,
ШчЙћЁЯBOC=nЁуЪБ,
ЁЯAOD=ЁЯCOD+ЁЯAOC=ЁЯCOD+(90ЁуЃЁЯCOB)= 90Ёу+(90ЁуЃnЁу)= 180ЁуЃnЁу,
(2)ИљОнНЧЕФКЭВюЙиЯЕНјааМЦЫуПЩЕУ:
ЁЯBOC=ЁЯAODЃЁЯDOBЃЁЯAOC =ЁЯAODЃ(ЁЯDOCЃЁЯCOB)Ѓ(ЁЯAOBЃЁЯCOB),
ЫљвдЁЯBOC=ЁЯAODЃЁЯDOC+ЁЯCOBЃЁЯAOB+ЁЯCOB,
ЫљвдЁЯBOC=ЁЯDOC+ЁЯAOBЃЁЯAOD,
ШчЙћЁЯAOB=ЁЯDOC=xЁу,ЁЯAOD=yЁу,
ЫљвдЁЯBOC= 2xЁуЃyЁу.
ЪдЬтНтЮі:(1)ШчЙћЁЯBOC=60Ёу,ФЧУДЁЯAOD=180Ёу-60Ёу=120Ёу,
ШчЙћЁЯBOC=nЁу,ФЧУДЁЯAOD=180Ёу-nЁу,
(2)вђЮЊЁЯAOB=ЁЯDOC=xЁу,ЁЯAOD=yЁу,
ЧвЁЯAOD=ЁЯAOB+ЁЯDOC-ЁЯBOC,ЫљвдЁЯBOC=ЁЯAOB+ЁЯDOC-ЁЯAOD=2xЁу-yЁу.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЋЫОЕк4дТЗнЭЖШы1000ЭђдЊПЦбаОЗб,МЦЛЎ6дТЗнЭЖШыПЦбаОЗбБШ4дТЖр500ЭђдЊ.ЩшИУЙЋЫОЕк5ЁЂ6ИідТЭЖЗХПЦбаОЗбЕФдТЦНОљдіГЄТЪЮЊx,дђЫљСаЗНГЬе§ШЗЕФЮЊ( )
A. 1000(1+x)2=1000+500
B. 1000(1+x)2=500
C. 500(1+x)2=1000
D. 1000(1+2x)=1000+500
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИљОнИјГіЕФЪ§жсМАвбжЊЬѕМўЃЌНтД№ЯТУцЕФЮЪЬтЃК
![]()
ЃЈ1ЃЉвбжЊЕуAЃЌBЃЌCБэЪОЕФЪ§ЗжБ№ЮЊ1ЃЌЉ2.5ЃЌЉ3ЙлВьЪ§жсЃЌгыЕуAЕФОрРыЮЊ3ЕФЕуБэЪОЕФЪ§ЪЧЁЁЁЁЃЌBЃЌCСНЕужЎМфЕФОрРыЮЊЁЁЁЁЃЛ
ЃЈ2ЃЉШєНЋЪ§жселЕўЃЌЪЙЕУAЕугыCЕужиКЯЃЌдђгыBЕужиКЯЕФЕуБэЪОЕФЪ§ЪЧЁЁЁЁЃЛШєДЫЪ§жсЩЯMЃЌNСНЕужЎМфЕФОрРыЮЊ2015ЃЈMдкNЕФзѓВрЃЉЃЌЧвЕБAЕугыCЕужиКЯЪБЃЌMЕугыNЕувВЧЁКУжиКЯЃЌдђMЃЌNСНЕуБэЪОЕФЪ§ЗжБ№ЪЧЃКMЁЁЁЁЃЌNЁЁЃЛ
ЃЈ3ЃЉШєЪ§жсЩЯPЃЌQСНЕуМфЕФОрРыЮЊmЃЈPдкQзѓВрЃЉЃЌБэЪОЪ§nЕФЕуЕНPЃЌQСНЕуЕФОрРыЯрЕШЃЌдђНЋЪ§жселЕўЃЌЪЙЕУPЕугыQЕужиКЯЪБЃЌPЃЌQСНЕуБэЪОЕФЪ§ЗжБ№ЮЊЃКPЁЁЁЁЃЌQЁЁЁЁЃЈгУКЌmЃЌnЕФЪНзгБэЪОетСНИіЪ§ЃЉ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЯпЖЮAB=20 cm,жБЯпABЩЯгавЛЕуC,ЧвBC=6 cm,ЕуMЪЧЯпЖЮABЕФжаЕу,ЕуNЪЧЯпЖЮBCЕФжаЕу,дђMN=____________ cm.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП(2016ЙуЖЋЪЁУЏУћЪаЕк20Ьт)гаЫФеХе§УцЗжБ№БъгаЪ§зж1ЃЌ2ЃЌ3ЃЌ4ЕФВЛЭИУїПЈЦЌЃЌЫќУЧГ§Ъ§зжЭтЦфгрШЋВПЯрЭЌЃЌЯжНЋЫќУЧБГУцГЏЩЯЯДОљдШЃЎ
ЃЈ1ЃЉЫцЛњГщШЁвЛеХПЈЦЌЃЌЧѓГщЕНЪ§зжЁА2ЁБЕФИХТЪЃЛ
ЃЈ2ЃЉЫцЛњГщШЁвЛеХПЈЦЌЃЌШЛКѓВЛЗХЛиЃЌдйЫцЛњГщШЁвЛеХПЈЦЌЃЌЧыгУСаБэЛђЛЪїзДЭМЕФЗНЗЈЧѓГіЕквЛДЮГщЕНЪ§зжЁА1ЁБЧвЕкЖўДЮГщЕНЪ§зжЁА2ЁБЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
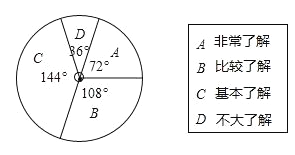
ЁОЬтФПЁП(2016еуНЪЁЮТжнЪаЕк18Ьт)ЮЊСЫНтбЇЩњЖдЁАРЌЛјЗжРрЁБжЊЪЖЕФСЫНтГЬЖШЃЌФГбЇаЃЖдБОаЃбЇЩњНјааГщбљЕїВщЃЌВЂЛцжЦЭГМЦЭМЃЌЦфжаЭГМЦЭМжаУЛгаБъзЂЯргІШЫЪ§ЕФАйЗжБШЃЎЧыИљОнЭГМЦЭМЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧѓЁАЗЧГЃСЫНтЁБЕФШЫЪ§ЕФАйЗжБШЃЎ
ЃЈ2ЃЉвбжЊИУаЃЙВга1200УћбЇЩњЃЌЧыЙРМЦЖдЁАРЌЛјЗжРрЁБжЊЪЖДяЕНЁАЗЧГЃСЫНтЁБКЭЁАБШНЯСЫНтЁБГЬЖШЕФбЇЩњЙВгаЖрЩйШЫЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЕуMЃЈ3ЃЌ1ЃЉЙигкyжсЕФЖдГЦЕуЕФзјБъЮЊЃЈЁЁЁЁЃЉ
A.ЃЈЉ3ЃЌ1ЃЉB.ЃЈ3ЃЌЉ1ЃЉC.ЃЈЉ3ЃЎЉ1ЃЉD.ЃЈ1ЃЌ3ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЦНУцжБНЧзјБъЯЕФкЕФЕуAЃЈЉ2ЃЌ3ЃЉЙигкдЕуЖдГЦЕФЕуЕФзјБъЪЧЃЈ ЃЉ
A.ЃЈ3ЃЌ2ЃЉ
B.ЃЈ2ЃЌЉ3ЃЉ
C.ЃЈ2ЃЌ3ЃЉ
D.ЃЈЉ2ЃЌЉ3ЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com