
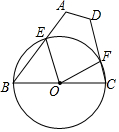
 如图,四边形ABCD两边AB,CD与以BC为直径的圆O分别交于点E、F,若∠A=135°,∠D=∠120°,BC=4,则扇形BOE与扇形COF的面积之和为$\frac{5π}{3}$.
如图,四边形ABCD两边AB,CD与以BC为直径的圆O分别交于点E、F,若∠A=135°,∠D=∠120°,BC=4,则扇形BOE与扇形COF的面积之和为$\frac{5π}{3}$. 分析 先求出∠B+∠C=105°,进而求出∠EOF,再用半圆的面积减去扇形EOF的面积即可.
解答 解:在四边形ABCD中,∠A=135°,∠D=∠120°,
∴∠B+∠C=105°,
∵OB=OE,OC=OF,
∴∠B=∠OEB,∠C=∠OFC,
∴∠BOE+∠COF=360°-2(∠B+∠C)=150°,
∴∠EOF=30°,
∴扇形BOE与扇形COF的面积之和为$\frac{1}{2}$S⊙O-S扇形EOF=$\frac{1}{2}$×π×22-$\frac{30°π×{2}^{2}}{360°}$=$\frac{5π}{3}$,
故答案为:$\frac{5π}{3}$.
点评 此题是圆周角定理,主要考查了四边形的内角和和等腰三角形的内角,扇形的面积公式,转化成半圆的面积减去扇形EOF的面积是解本题的关键.


科目:初中数学 来源:2016-2017学年江苏省苏州太仓市第二学期初一期中模拟数学试卷(解析版) 题型:解答题
某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)求该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性定客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
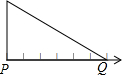 慧慧自己做了一个三角形的纸板,并在其中一边画了七个等距离的小黑点,每相邻两个小黑点之间的距离为1个单位长度,现把此边放在如图所示的数轴上,若点P所表示的数是-1.6,则点Q所表示的数是4.4.
慧慧自己做了一个三角形的纸板,并在其中一边画了七个等距离的小黑点,每相邻两个小黑点之间的距离为1个单位长度,现把此边放在如图所示的数轴上,若点P所表示的数是-1.6,则点Q所表示的数是4.4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
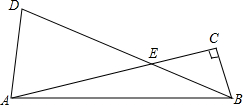 在Rt△ABC中,∠CAB=α,斜边AB绕点B顺时针旋转2α角度得到DB,交AC于点E,连接AD,记AD=kBE.
在Rt△ABC中,∠CAB=α,斜边AB绕点B顺时针旋转2α角度得到DB,交AC于点E,连接AD,记AD=kBE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
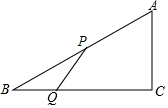 如图,在直角三角形ABC中,直角边AC=3cm,BC=4cm.设P、Q分别为AB、BC上的动点,在点P自点A沿AB方向向点B作匀速移动的同时,点Q自点B沿BC方向向点C作匀速移动,它们移动的速度均为每秒1cm,当Q点到达C点时,P点就停止移动.设P、Q移动的时间t秒.
如图,在直角三角形ABC中,直角边AC=3cm,BC=4cm.设P、Q分别为AB、BC上的动点,在点P自点A沿AB方向向点B作匀速移动的同时,点Q自点B沿BC方向向点C作匀速移动,它们移动的速度均为每秒1cm,当Q点到达C点时,P点就停止移动.设P、Q移动的时间t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
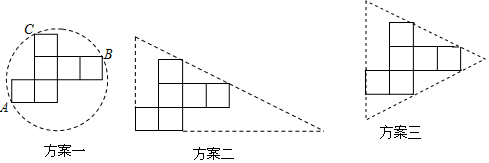
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
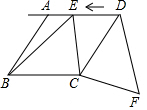 如图,两个边长为6的等边三角形拼出四边形ABCD,点E从点D出发,以每秒1个单位长度的速度沿着射线DA的方向匀速运动,设运动时间为t秒.将线段CE绕点C顺时针旋转一个角α(α=∠BCD),得到对应线段CF.当t=9时,DF的长度有最小值,最小值等于3$\sqrt{3}$.
如图,两个边长为6的等边三角形拼出四边形ABCD,点E从点D出发,以每秒1个单位长度的速度沿着射线DA的方向匀速运动,设运动时间为t秒.将线段CE绕点C顺时针旋转一个角α(α=∠BCD),得到对应线段CF.当t=9时,DF的长度有最小值,最小值等于3$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
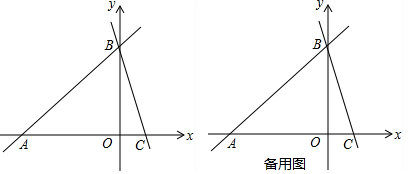
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 次数m | 余额n(元) |
| 1 | 50-0.8 |
| 2 | 50-1.6 |
| 3 | 50-2.4 |
| 4 | 50-3.2 |
| … | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com