
 如图,直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)交于不同的两点A(x1,x2),B(x2,y2),与x轴交于点P(x0,0),与y轴交于点C.
如图,直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)交于不同的两点A(x1,x2),B(x2,y2),与x轴交于点P(x0,0),与y轴交于点C.分析 (1)由b=3即点P坐标(6,0)可得出直线的解析式,令y=ax+b=$\frac{k}{x}$,解关于x的方程,即可得出x1、x2的值,结合AB=BP即可得出关于k的方程,解方程即可得出k值,代入到x1、x2中即可得出A、B的横坐标,结合直线的解析式即能得出结论;
(2)猜测x1+x2=x0.令y=ax+b=$\frac{k}{x}$,用含a、b、k的代数式来表示出x1、x2,再令直线y=ax+b=0,用a、b表示出来x0,将x1、x2相加即可证明结论成立.
解答 解:(1)当b=3,x0=6时,点P的坐标为(6,0),
将点P代入y=ax+3中得:0=6a+3,
解得:a=-$\frac{1}{2}$.
∴直线的解析式为y=-$\frac{1}{2}$x+3.
令y=-$\frac{1}{2}$x+3=$\frac{k}{x}$,即$\frac{1}{2}$x2-3x+k=0,
解得:x1=$\frac{-(-3)-\sqrt{9-2k}}{2×\frac{1}{2}}$=3-$\sqrt{9-2k}$,x2=3+$\sqrt{9-2k}$,
∵AB=BP,
∴3+$\sqrt{9-2k}$-(3-$\sqrt{9-2k}$)=6-(3+$\sqrt{9-2k}$),
解得:k=4.
此时x1=2,x2=4,
故点A的坐标为(2,2),点B的坐标为(4,1).
(2)猜测x1+x2=x0.
证明:(方法一)令y=ax+b=$\frac{k}{x}$,即ax2+bx-k=0,
解得:x1=$\frac{-b-\sqrt{{b}^{2}+4ak}}{2a}$,x2=$\frac{-b+\sqrt{{b}^{2}+4ak}}{2a}$.
令y=ax+b=0,解得:x0=-$\frac{b}{a}$.
∴x1+x2=$\frac{-b-\sqrt{{b}^{2}+4ak}}{2a}$+$\frac{-b+\sqrt{{b}^{2}+4ak}}{2a}$=-$\frac{b}{a}$=x0.
(方法二)令y=ax+b=$\frac{k}{x}$,即ax2+bx-k=0,
则x1+x2=-$\frac{b}{a}$.
令y=ax+b=0,解得:x0=-$\frac{b}{a}$.
∴x1+x2=x0=-$\frac{b}{a}$.
点评 本题考查了反比例函数与一次函数的交点问题以及求根公式,解题的关键是:(1)结合AB=BP得出关于k的方程;(2)用求根公式表示出来x1、x2,再令y=0找出x0.本题属于中档题,难度不大,解决该题型题目时,由求根公式表示出x的值是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省句容市华阳片八年级下学期第一次月考数学试卷(解析版) 题型:单选题
顺次连结矩形四边的中点所得的四边形是( )
A. 矩形 B. 正方形 C. 菱形 D. 以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省句容市华阳片八年级下学期第一次月考数学试卷(解析版) 题型:填空题
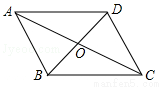
如图,□ABCD的对角线交于点O,且AB=5,△OCD的周长为13,则□ABCD的两条对角线长度之和为________.
查看答案和解析>>
科目:初中数学 来源:2017届陕西省宝鸡市渭滨区九年级上学期期末考试数学试卷(解析版) 题型:填空题
一个布袋内只装有一个红球和2个黄球,这些球除颜色外其余都相同,随机摸出一个球后放回搅匀,再随机摸出一个球,则两次摸出的球都是黄球的概率是____.
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省扬州市七年级下学期第一次月考数学试卷(解析版) 题型:单选题
下列运算正确的是( )
A. 3a2﹣a2=3 B. (a2)3=a5 C. a3•a6=a9 D. (2a2)2=4a2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com