
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:①ac<0;②当x>1时,y的值随x值的增大而减小.
③当x=2时,y=5;④3是方程ax2+(b﹣1)x+c=0的一个根;
其中正确的有 . (填正确结论的序号)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,过点A0(2,0)作直线l:y= ![]() x的垂线,垂足为点A1 , 过点A1作A1A2⊥x轴,垂足为点A2 , 过点A2作A2A3⊥l,垂足为点A3 , …,这样依次下去,得到一组线段:A0A1 , A1A2 , A2A3 , …,则线段A2016A2107的长为( )
x的垂线,垂足为点A1 , 过点A1作A1A2⊥x轴,垂足为点A2 , 过点A2作A2A3⊥l,垂足为点A3 , …,这样依次下去,得到一组线段:A0A1 , A1A2 , A2A3 , …,则线段A2016A2107的长为( )
A.( ![]() )2015
)2015
B.( ![]() )2016
)2016
C.( ![]() )2017
)2017
D.( ![]() )2018
)2018
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD被直线EF所截,∠1=55°,下列条件中能判定AB∥CD的是( ) 
A.∠2=35°
B.∠2=45°
C.∠2=55°
D.∠2=125°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+mx+3与x轴交于点A、B两点,与y轴交于C点,点B的坐标为(3,0),抛物线与直线y=﹣ ![]() x+3交于C、D两点.连接BD、AD.
x+3交于C、D两点.连接BD、AD. 
(1)求m的值.
(2)抛物线上有一点P,满足S△ABP=4S△ABD , 求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,斜边AB=9,D为AB的中点,F为CD上一点,且CF= ![]() CD,过点B作BE∥DC交AF的延长线于点E,则BE的长为( )
CD,过点B作BE∥DC交AF的延长线于点E,则BE的长为( ) 
A.6
B.4
C.7
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的直径CD=6,A,B为圆周上两点,且四边形OABC是平行四边形,过A点作直线EF∥BD,分别交CD,CB的延长线于点E,F,AO与BD交于G点. 
(1)求证:EF是⊙O的切线;
(2)求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班为满足同学们课外活动的需求,要求购排球和足球若干个.已知足球的单价比排球的单价多30元,用500元购得的排球数量与用800元购得的足球数量相等.
(1)排球和足球的单价各是多少元?
(2)若恰好用去1200元,有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1.把△ABC分别绕直线AB和BC旋转一周,所得几何体的地面圆的周长分别记作l1 , l2 , 侧面积分别记作S1 , S2 , 则( )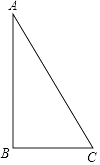
A.l1:l2=1:2,S1:S2=1:2
B.l1:l2=1:4,S1:S2=1:2
C.l1:l2=1:2,S1:S2=1:4
D.l1:l2=1:4,S1:S2=1:4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为一个矩形纸片,AB=3,BC=2,动点P自D点出发沿DC方向运动至C点后停止,△ADP以直线AP为轴翻折,点D落在点D1的位置,设DP=x,△AD1P与原纸片重叠部分的面积为y.
(1)当x为何值时,直线AD1过点C?
(2)当x为何值时,直线AD1过BC的中点E?
(3)求出y与x的函数表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com