
【题目】已知实数a,c满足![]() ,2a+c﹣ac+2>0,二次函数y=ax2+bx+9a经过点B(4,n)、A(2,n),且当1≤x≤2时,y=ax2+bx+9a的最大值与最小值之差是9,求a的值.
,2a+c﹣ac+2>0,二次函数y=ax2+bx+9a经过点B(4,n)、A(2,n),且当1≤x≤2时,y=ax2+bx+9a的最大值与最小值之差是9,求a的值.
【答案】3
【解析】
根据题意求得a>-2,b=-6a,得出y=a(x-3)2,根据对称轴公式求出b=﹣6a,然后根据当1≤x≤2时,y=ax2+bx+9a的最大值与最小值之差是9,列出方程,解方程即可求得.
∵实数a,c满足![]() ,
,
∴c﹣ac=﹣a.
∵2a+c﹣ac+2>0,
∴2a﹣a+2>0,
∴a>﹣2.
∵二次函数y=ax2+bx+9a经过点B(4,n),A(2,n),
∴![]() ,
,
∴b=﹣6a,
∴y=ax2+bx+9a=a(x2﹣6x+9)=a(x﹣3)2
当x=1时,y=4a;当x=2时,y=a
∵当1≤x≤2时,y=ax2+bx+9a的最大值与最小值之差是9,
∴|4a﹣a|=9,
∴a=3或-3,
又∵a>﹣2
∴a=3


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC,BD是对角线,△ABC是等边三角形.线段CD绕点C顺时针旋转60°得到线段CE,连接AE.
(1)求证:AE=BD;
(2)若∠ADC=30°,AD=3,BD=4![]() .求CD的长.
.求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=![]() .下列结论:
.下列结论:
①△ADE∽△ACD; ②当BD=6时,△ABD与△DCE全等;
③△DCE为直角三角形时,BD为8; ④0<CE≤6.4.
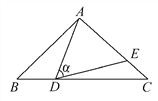
其中正确的结论是____________.(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=x2﹣6x﹣16,AB为半圆的直径,则这个“果圆”被y轴截得的线段CD的长为_____.
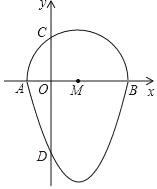
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】10个人围成一个圆圈做游戏,游戏的规则是:每个人心里都想好一个数,并把自己想好的数如实地告诉与他相邻的两个人,然后每个人将与他相邻的两个人告诉他的数的平均数报出来,若报出来的数如图所示,则报2的人心里想的数是____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小刚玩“石头、剪刀、布”的游戏,每一局游戏双方各自随机做出“石头”、“剪刀”、“布”三种手势的一种,规定“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,相同的手势是和局.
(1)用树形图或列表法计算在一局游戏中两人获胜的概率各是多少?
(2)如果两人约定:只要谁率先胜两局,就成了游戏的赢家.用树形图或列表法求只进行两局游戏便能确定赢家的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AC的中点,连接BD,按以下步骤作图:①分别以B,D为圆心,大于![]() BD的长为半径作弧,两弧相交于点P和点Q;②作直线PQ交AB于点E,交BC于点F,则BF=( )
BD的长为半径作弧,两弧相交于点P和点Q;②作直线PQ交AB于点E,交BC于点F,则BF=( )
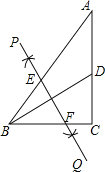
A. ![]() B. 1C.
B. 1C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
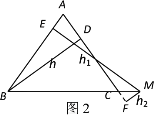
【题目】(阅读)如图1,在等腰△ABC中,AB=AC,AC边上的高为h,M是底边BC上的任意一点,点M到腰AB、AC的距离分别为h1,h2.连接AM.
∵![]() ∴
∴![]()
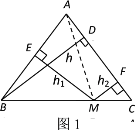
(思考)在上述问题中,h1,h2与h的数量关系为: .
(探究)如图2,当点M在BC延长线上时,h1、h2、h之间有怎样的数量关系式?并说明理由.
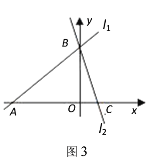
(应用)如图3,在平面直角坐标系中有两条直线l1:![]() ,l2:y=-3x+3,若l2上的一点M到l1的距离是1,请运用上述结论求出点M的坐标.
,l2:y=-3x+3,若l2上的一点M到l1的距离是1,请运用上述结论求出点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com