
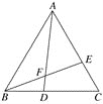
【题目】如图所示,△ABC是等边三角形,点D、E分别在BC、AC上,且CE=BD,BE、AD相交于点F.求证:
(1)△ABD≌△BCE;
(2)△AEF∽△ABE.
【答案】(1)见解析;(2)见解析.
【解析】
(1)由△ABC 是等边三角形,根据等边三角形的性质可得: AB=BC , ∠ABD=∠C=∠BAC=60°,继而根据SAS即可证得△ABD≌△BCE ;
(2)由△ABD≌△BCE ,可证得∠BAD=∠CBE ,进一步得到∠EAF=∠ABE ,然后根据有两角对应相等的三角形相似,即可得△AEF∽△ABE .
证明 (1)∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠C=∠BAC=60°,
在△ABD和△BCE中,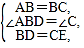
∴△ABD≌△BCE(SAS);
(2)∵△ABD≌△BCE,
∴∠BAD=∠CBE,
∴∠EAF=∠ABE,
∵∠AEF=∠BEA,
∴△AEF∽△ABE.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ACB=90°,D是边AB的中点,P是边AC上一动点,BP与CD相交于点E.
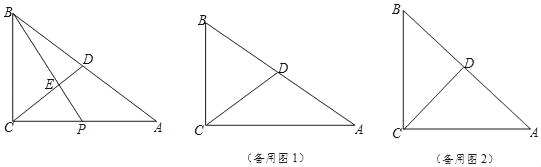
(1)如果BC=6,AC=8,且P为AC的中点,求线段BE的长;
(2)联结PD,如果PD⊥AB,且CE=2,ED=3,求cosA的值;
(3)联结PD,如果BP2=2CD2,且CE=2,ED=3,求线段PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,□ABCD的对角线AC,BD相交于点O,E、F、G、H分别是OA、OB、OC、OD的中点,那么□ABCD与四边形EFGH是否是位似图形?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
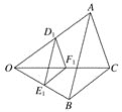
【题目】如图,O点是△ABC与△D1E1F1的位似中心,△ABC的周长为1.若D1、E1、F1分别是线段OA、OB、OC的中点,则△D1E1F1的周长为![]() ;若OD2=
;若OD2=![]() OA、OE2=
OA、OE2=![]() OB、OF2=
OB、OF2=![]() OC,则△D2E2F2的周长为
OC,则△D2E2F2的周长为![]() ;…若ODn=
;…若ODn=![]() OA、OEn=
OA、OEn=![]() OB、OFn=
OB、OFn=![]() OC,则△DnEnFn的周长为__________.(用正整数n表示)
OC,则△DnEnFn的周长为__________.(用正整数n表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为45°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为110m,那么该建筑物的高度BC约为_____m(结果保留整数,![]() ≈1.73).
≈1.73).
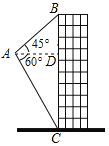
查看答案和解析>>
科目:初中数学 来源: 题型:
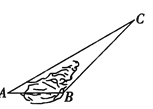
【题目】如图,A,B两地之间有一座山,汽车原来从A地到B地需经C地沿折线ACB行驶,现开通隧道后,汽车直接沿直线AB行驶即可到达B地.已知AC=120km,∠A=30°,∠B=135°,求隧道开通后汽车从A地到B地需行驶多少千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
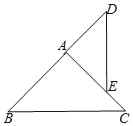
【题目】如图,△ABC与△ADE都是等腰直角三角形,且它们的底分别是BC=5,DE=3,则△ABC与△ADE的面积比为( )
A. ![]() :
:![]() B. 25:9 C. 5:3 D. 5
B. 25:9 C. 5:3 D. 5![]() :3
:3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价分别为2000元、1700元的A、B两种型号的空调,如表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 18000元 |
第二周 | 4台 | 10台 | 31000元 |
(进价、售价均保持不变,利润=销售总收入进货成本)
(1)求A、B两种型号的空调的销售单价;
(2)若超市准备用不多于54000元的金额再采购这两种型号的空调共30台,求A种型号的空调最多能采购多少台?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com