
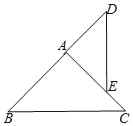
【题目】如图,△ABC与△ADE都是等腰直角三角形,且它们的底分别是BC=5,DE=3,则△ABC与△ADE的面积比为( )
A. ![]() :
:![]() B. 25:9 C. 5:3 D. 5
B. 25:9 C. 5:3 D. 5![]() :3
:3![]()
【答案】B
【解析】
过A作AG⊥BC于G, AH⊥DE于H,利用角平分线的性质得到∠GAH=90°,进而结合平行线的性质得出△AGC∽△EHA,再利用相似三角形的面积比等于相似比的平方即可得到结论
解:过A作AG⊥BC于G, AH⊥DE于H,
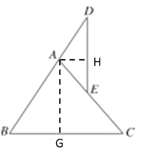
∴AG平分∠BAC,AH平分∠DAE, ∴∠EAH=![]() ∠DAE, ∠GAC=
∠DAE, ∠GAC=![]() ∠BAC, ∵∠DAE+∠BAC=180°, ∴∠EAH+∠DAE=90°, 即∠GAH=90°,∴∠GAH=∠AHE=90°, ∴AG∥DE, ∴∠GAC=∠AEH, ∵∠AGC=∠AHE=90°, ∴△AGC∽△EHA, ∴
∠BAC, ∵∠DAE+∠BAC=180°, ∴∠EAH+∠DAE=90°, 即∠GAH=90°,∴∠GAH=∠AHE=90°, ∴AG∥DE, ∴∠GAC=∠AEH, ∵∠AGC=∠AHE=90°, ∴△AGC∽△EHA, ∴![]() ∶
∶![]() =CG∶EH=25∶9, ∵
=CG∶EH=25∶9, ∵![]() , ∴
, ∴![]() ∶
∶![]() =25∶9
=25∶9
故选B.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】即墨素有“中国针织名城”的美誉,2016年,又被中国服装协会授予“中国童装名称”的称号,该区一网店销售某款童装,当每件售价80元时,每周可卖200件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖20件.已知该款童装每件成本价60元,设该款童装每件售价x(60≤x≤80)元,每周的销售量为y件.
(1)求y与x之间的函数关系式;
(2)设每周的销售利润为W元,当每件售价定为多少元时,每周的销售利润最大,最大利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
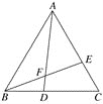
【题目】如图所示,△ABC是等边三角形,点D、E分别在BC、AC上,且CE=BD,BE、AD相交于点F.求证:
(1)△ABD≌△BCE;
(2)△AEF∽△ABE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知双曲线![]() ,经过点D(6,1),点C是双曲线第三象限上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.
,经过点D(6,1),点C是双曲线第三象限上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.
(1)求k的值;
(2)若△BCD的面积为12,求直线CD的解析式;
(3)判断AB与CD的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5,另外每天还需支付其他各项费用80元.
销售单价x(元) | 3.5 | 5.5 |
销售量y(袋) | 280 | 120 |
(1)请直接写出y与x之间的函数关系式;
(2)如果每天获得160元的利润,销售单价为多少元?
(3)设每天的利润为w元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
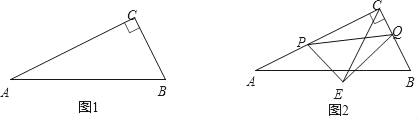
【题目】如图1,在Rt△ABC中,∠ACB=90°,AC=10cm,BC=5cm,点P从点C出发沿线段CA以每秒2cm的速度运动,同时点Q从点B出发沿线段BC以每秒1cm的速度运动.设运动时间为t秒(0<t<5).
(1)填空:AB= cm;
(2)t为何值时,△PCQ与△ACB相似;
(3)如图2,以PQ为斜边在异于点C的一侧作Rt△PEQ,且![]() ,连结CE,求CE.(用t的代数式表示).
,连结CE,求CE.(用t的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ACB中,∠C=90°,AC=BC,一直角三角板的直角顶角O在AB边的中点上,这块三角板绕O点旋转,两条直角边始终与AC、BC边分别相交于E、F,连接EF,则在运动过程中,△OEF与△ABC的关系是( )
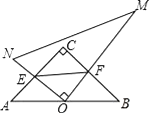
A. 一定相似 B. 当E是AC中点时相似
C. 不一定相似 D. 无法判断
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,规定:抛物线![]() 的伴随直线为
的伴随直线为![]() .例如:抛物线
.例如:抛物线![]() 的伴随直线为
的伴随直线为![]() ,即y=2x﹣1.
,即y=2x﹣1.
(1)在上面规定下,抛物线![]() 的顶点坐标为 ,伴随直线为 ,抛物线
的顶点坐标为 ,伴随直线为 ,抛物线![]() 与其伴随直线的交点坐标为 和 ;
与其伴随直线的交点坐标为 和 ;
(2)如图,顶点在第一象限的抛物线![]() 与其伴随直线相交于点A,B(点A在点B的左侧),与x轴交于点C,D.
与其伴随直线相交于点A,B(点A在点B的左侧),与x轴交于点C,D.
①若∠CAB=90°,求m的值;

②如果点P(x,y)是直线BC上方抛物线上的一个动点,△PBC的面积记为S,当S取得最大值![]() 时,求m的值.
时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
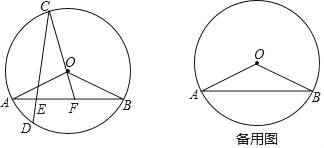
【题目】如图,在⊙O中,弦AB、CD相交于点E,![]() =
=![]() ,点D在
,点D在![]() 上,连接CO,并延长CO交线段AB于点F,连接OA、OB,且OA=
上,连接CO,并延长CO交线段AB于点F,连接OA、OB,且OA=![]() ,tan∠OBA=
,tan∠OBA=![]() .
.
(1)求证:∠OBA=∠OCD;
(2)当△AOF是直角三角形时,求EF的长;
(3)是否存在点F,使得S△CEF=4S△BOF,若存在,请求EF的长,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com