
【题目】在平面直角坐标系中,规定:抛物线![]() 的伴随直线为
的伴随直线为![]() .例如:抛物线
.例如:抛物线![]() 的伴随直线为
的伴随直线为![]() ,即y=2x﹣1.
,即y=2x﹣1.
(1)在上面规定下,抛物线![]() 的顶点坐标为 ,伴随直线为 ,抛物线
的顶点坐标为 ,伴随直线为 ,抛物线![]() 与其伴随直线的交点坐标为 和 ;
与其伴随直线的交点坐标为 和 ;
(2)如图,顶点在第一象限的抛物线![]() 与其伴随直线相交于点A,B(点A在点B的左侧),与x轴交于点C,D.
与其伴随直线相交于点A,B(点A在点B的左侧),与x轴交于点C,D.
①若∠CAB=90°,求m的值;

②如果点P(x,y)是直线BC上方抛物线上的一个动点,△PBC的面积记为S,当S取得最大值![]() 时,求m的值.
时,求m的值.
【答案】(1)(-1,-4);y=x-3;(0,-3);(-1,-4);)(2)①m=-![]() ; ②m=-2
; ②m=-2
【解析】试题分析:(1)、由抛物线的顶点式可求得其顶点坐标,由伴随直线的定义可求得伴随直线的解析式,联立伴随直线和抛物线解析式可求得其交点坐标;(2)、①、可先用m表示出A、B、C、D的坐标,利用勾股定理可表示出AC2、AB2和BC2,在Rt△ABC中由勾股定理可得到关于m的方程,可求得m的值;②、由B、C的坐标可求得直线BC的解析式,过P作x轴的垂线交BC于点Q,则可用x表示出PQ的长,进一步表示出△PBC的面积,利用二次函数的性质可得到m的方程,可求得m的值.
试题解析:(1)、(-1,-4);y=x-3;(0,-3);(-1,-4)
(2)、①因为抛物线解析式为![]() ,所以其伴随直线为
,所以其伴随直线为![]() ,即
,即![]() 。
。
联立抛物线与伴随直线的解析式可得:![]() ,解得
,解得![]() 或
或![]() ,所以
,所以![]() ,
,![]() ,
,
在![]() 中,令
中,令![]() 可计算出
可计算出![]() 或
或![]() ,所以
,所以![]() ,
,![]() ,
,
即![]() ,
,![]() ,
,![]() ,
,
若![]() ,则
,则![]() ,即
,即![]() ,
,
解得:![]() (抛物线开口向下,舍去),
(抛物线开口向下,舍去),![]() ,
,
所以当![]() 时,
时,![]() ;
;
②设直线![]() 的解析式为
的解析式为![]() ,如图过
,如图过![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 于点
于点![]() ,如图所示:
,如图所示:
因为点![]() 的横坐标为
的横坐标为![]() ,所以
,所以![]() ,
,![]() ,因为
,因为![]() 是直线
是直线![]() 上方抛物线上的一个动点,
上方抛物线上的一个动点,
所以![]()
![]()
![]() ,
,
所以,![]() 。
。
当![]() 时,
时,![]() 的值有最大值
的值有最大值![]() ,所以
,所以![]() 取得最大值
取得最大值![]() 时,即
时,即![]() ,计算得出
,计算得出![]() .
.


科目:初中数学 来源: 题型:
【题目】有A、B两组卡片共5张,A组的三张分别写有数字2,4,6,B组的两张分别写有3,5.它们除了数字外没有任何区别,
(1)随机从A组抽取一张,求抽到数字为2的概率;
(2)随机地分别从A组、B组各抽取一张,请你用列表或画树状图的方法表示所有等可能的结果.现制定这样一个游戏规则:若选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,现同时将点
,现同时将点![]() ,
,![]() 分别向上平移2个单位,再向右平移1个单位,分别得到点
分别向上平移2个单位,再向右平移1个单位,分别得到点![]() ,
,![]() 的对应点
的对应点![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
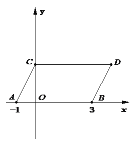
(1)求点![]() ,
,![]() 的坐标及四边形
的坐标及四边形![]() 的面积
的面积![]()
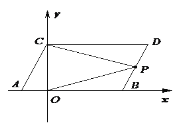
(2)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,连接
,连接![]() ,
,![]() ,使
,使![]() ,若存在这样一点,求出点
,若存在这样一点,求出点![]() 的坐标,若不存在,试说明理由.
的坐标,若不存在,试说明理由.
(3)点![]() 是线段
是线段![]() 上的一个动点,连接
上的一个动点,连接![]() ,
,![]() ,当点
,当点![]() 在
在![]() 上移动时(不与
上移动时(不与![]() ,
,![]() 重合)给出下列结论:
重合)给出下列结论:
①![]() 的值不变,②
的值不变,② ![]() 的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学七年级同学到野外开展数学综合实践活动,在营地看到一池塘,同学们想知道池塘两端的距离.有一位同学设计了如下测量方案:先在平地上取一个可直接到达A、B的点E(A、B为池塘的两端),连接AE、BE并分别延长AE至D,BE至C,使ED=AE,EC=EB,测出CD的长作为AB之间的距离.
(1)他的方案可行吗?请说明理由.
(2)若测得CD=10m,则池塘两端的距离是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国西南五省市的部分地区发生严重旱灾,为鼓励节约用水,某市自来水公司采取分段收费标准,右图反映的是每月收取水费y(元)与用水量x(吨)之间的函数关系.
(1)小明家五月份用水8吨,应交水费______ 元;
(2)按上述分段收费标准,小明家三、四月份分别交水费26元和18元,问四月份比三月份节约用水多少吨?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个四位数![]() ,如果千位与十位上的数字之和为9,百位与个位上的数字之和也为9,则称
,如果千位与十位上的数字之和为9,百位与个位上的数字之和也为9,则称![]() 为“极数”;如果一个正整数
为“极数”;如果一个正整数![]() 是另一个正整数
是另一个正整数![]() 的平方,则称正整数
的平方,则称正整数![]() 是完全平方数.若四位数
是完全平方数.若四位数![]() 为“极数”,记
为“极数”,记![]() ,若
,若![]() 是完全平方数,则
是完全平方数,则![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步发展基础教育,自2014年以来,某县加大了教育经费的投入,2014年该县投入教育经费6000万元。2016年投入教育经费8640万元。假设该县这两年投入教育经费的年平均增长率相同。
(1)求这两年该县投入教育经费的年平均增长率;
(2)若该县教育经费的投入还将保持相同的年平均增长率,请你预算2017年该县投入教育经费多少万元。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列生活现象:
①用两个钉子就可以把木条固定在墙上;
②从![]() 地道
地道![]() 地架设电线,总是尽可能沿着线段
地架设电线,总是尽可能沿着线段![]() 架设;
架设;
③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线;
④把弯曲的公路改直,就能缩短路程.
其中能用“两点之间,线段最短”来解释的现象个数有( )
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com