
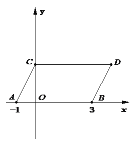
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,现同时将点
,现同时将点![]() ,
,![]() 分别向上平移2个单位,再向右平移1个单位,分别得到点
分别向上平移2个单位,再向右平移1个单位,分别得到点![]() ,
,![]() 的对应点
的对应点![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
(1)求点![]() ,
,![]() 的坐标及四边形
的坐标及四边形![]() 的面积
的面积![]()
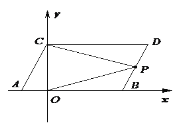
(2)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,连接
,连接![]() ,
,![]() ,使
,使![]() ,若存在这样一点,求出点
,若存在这样一点,求出点![]() 的坐标,若不存在,试说明理由.
的坐标,若不存在,试说明理由.
(3)点![]() 是线段
是线段![]() 上的一个动点,连接
上的一个动点,连接![]() ,
,![]() ,当点
,当点![]() 在
在![]() 上移动时(不与
上移动时(不与![]() ,
,![]() 重合)给出下列结论:
重合)给出下列结论:
①![]() 的值不变,②
的值不变,② ![]() 的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
【答案】(1)![]() ,
,![]() ;(2)(0,8)或(0,-8);(3)①;1.
;(2)(0,8)或(0,-8);(3)①;1.
【解析】
(1)根据向右平移横坐标加,向上平移纵坐标加写出点C、D的坐标即可,再根据平行四边形的面积公式列式计算即可得解;(2)设点P到AB的距离为h,根据已知条件S△PAB=2S四边形ABDC求得h的值,由此即可求得点P的坐标;(3)①是正确的结论,过点P作PQ∥CD,即可得PQ∥AB∥CD,由平行线的性质可得∠DCP=∠CPQ,∠BOP=∠OPQ,所以∠DCP+∠BOP=∠CPQ +∠OPQ =∠CPO,由此即可得![]() .
.
(1)∵点A(-1,0),B(3,0)分别向上平移2个单位,再向右平移1个单位,
∴点C、D的坐标分别为(0,2),(4,2),
S四边形ABDC=4×2=8;
(2)在y轴上存在一点P,使S△PAB=2S四边形ABDC.理由如下:
设点P到AB的距离为h,
S△PAB=![]() ×AB×h=2h,
×AB×h=2h,
由S△PAB=2S四边形ABDC,得2h=16,
解得h=8,
∴P(0,8)或(0,-8).
(3)①是正确的结论,过点P作PQ∥CD,
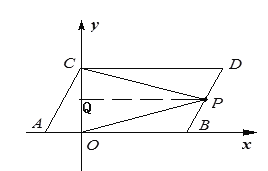
∵AB∥CD,
∴PQ∥AB∥CD(平行公理的推论)
∴∠DCP=∠CPQ,∠BOP=∠OPQ,
∴∠DCP+∠BOP=∠CPQ +∠OPQ =∠CPO,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】矩形ABCD中,点E、F分别在边CD、AB上,且DE=BF,∠ECA=∠FCA.
(1)求证:四边形AFCE是菱形;
(2)若AB=8,BC=4,求菱形AFCE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场准备进一批两种不同型号的衣服,已知购进A种型号衣服9件,B种型号衣服10件,则共需1810元;若购进A种型号衣服12件,B种型号衣服8件,共需1880元;已知销售一件A型号衣服可获利18元,销售一件B型号衣服可获利30元,要使在这次销售中获利不少于699元,且A型号衣服不多于28件.
(1)求A、B型号衣服进价各是多少元?
(2)若已知购进A型号衣服是B型号衣服的2倍还多4件,则商店在这次进货中可有几种方案并简述购货方案.
【答案】(1)A种型号的衣服每件90元,B种型号的衣服100元;(2)有三种进货方案,具体见解析.
【解析】试题分析:(1)等量关系为:A种型号衣服9件×进价+B种型号衣服10件×进价=1810,A种型号衣服12件×进价+B种型号衣服8件×进价=1880;
(2)关键描述语是:获利不少于699元,且A型号衣服不多于28件.关系式为:18×A型件数+30×B型件数≥699,A型号衣服件数≤28.
试题解析:(1)设A种型号的衣服每件x元,B种型号的衣服y元,
则:![]() ,
,
解之得![]() .
.
答:A种型号的衣服每件90元,B种型号的衣服100元;
(2)设B型号衣服购进m件,则A型号衣服购进(2m+4)件,
可得:![]() ,
,
解之得192m12,
∵m为正整数,
∴m=10、11、12,2m+4=24、26、28.
答:有三种进货方案:
(1)B型号衣服购买10件,A型号衣服购进24件;
(2)B型号衣服购买11件,A型号衣服购进26件;
(3)B型号衣服购买12件,A型号衣服购进28件。
点睛:点睛:本题主要考查二元一次方程组和一元一次不等式组的实际问题的应用,解题的关键是读懂题目的意思,根据题目给出的条件,设出未知数,分别找出甲组和乙组对应的工作时间,找出合适的等量关系,列出方程组,再求解.
【题型】解答题
【结束】
21
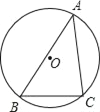
【题目】如图,锐角△ABC内接于⊙O,若⊙O的半径为6,sinA=![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
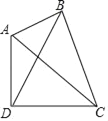
【题目】如图,四边形ABCD中,AC、BD是它的对角线,∠ABC=∠ADC=90°,∠BCD是锐角.
(1)若BD=BC,证明:sin∠BCD=![]() .
.
(2)若AB=BC=4,AD+CD=6,求![]() 的值.
的值.
(3)若BD=CD,AB=6,BC=8,求sin∠BCD的值.
(注:本题可根据需要自己画图并解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面的三角形中:①△ABC中,∠C=∠A-∠B;②△ABC中,∠A:∠B:∠C=1:2:3;③△ABC中,a:b:c=5:12:13; ④△ABC中,三边长分别为![]() ;其中,直角三角形的个数有( ).
;其中,直角三角形的个数有( ).
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC=( )
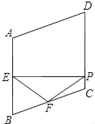
A. 35°B. 45°C. 50°D. 55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,规定:抛物线![]() 的伴随直线为
的伴随直线为![]() .例如:抛物线
.例如:抛物线![]() 的伴随直线为
的伴随直线为![]() ,即y=2x﹣1.
,即y=2x﹣1.
(1)在上面规定下,抛物线![]() 的顶点坐标为 ,伴随直线为 ,抛物线
的顶点坐标为 ,伴随直线为 ,抛物线![]() 与其伴随直线的交点坐标为 和 ;
与其伴随直线的交点坐标为 和 ;
(2)如图,顶点在第一象限的抛物线![]() 与其伴随直线相交于点A,B(点A在点B的左侧),与x轴交于点C,D.
与其伴随直线相交于点A,B(点A在点B的左侧),与x轴交于点C,D.
①若∠CAB=90°,求m的值;

②如果点P(x,y)是直线BC上方抛物线上的一个动点,△PBC的面积记为S,当S取得最大值![]() 时,求m的值.
时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
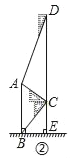
【题目】腾飞中学在教学楼前新建了一座“腾飞”雕塑(如图①).为了测量雕塑的高度,小明利用三角板测得雕塑顶端A点的仰角为30°,底部B点的俯角为45°,小华在五楼找到一点D,利用三角板测得A点的俯角为60°(如图②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据![]() =1.73).
=1.73).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com