
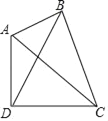
【题目】如图,四边形ABCD中,AC、BD是它的对角线,∠ABC=∠ADC=90°,∠BCD是锐角.
(1)若BD=BC,证明:sin∠BCD=![]() .
.
(2)若AB=BC=4,AD+CD=6,求![]() 的值.
的值.
(3)若BD=CD,AB=6,BC=8,求sin∠BCD的值.
(注:本题可根据需要自己画图并解答)
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】分析:
(1)如图1,过点B作BE⊥AD交AD的延长线于点E,由已知条件易得点A、B、C、D四点共圆,由此可得∠EAB=∠BCD,∠EDB=∠BCA,结合∠DEB=∠ABC=90°,可得△BED∽△ABC,从而可得sin∠BCD=sin∠EAB=![]() ,结合BD=BC即可得到所求结论;
,结合BD=BC即可得到所求结论;
(2)如图2中,过点B作BF⊥BD交DC的延长线于F.由已知条件通过证△DAB≌△CBF得到BD=BF,AD=CF,从而可得△DBF是等腰直角三角形,由此可得BD=![]() DF,结合DF=DC+CF=DC+AD=6即可求得BD的长,在Rt△ABC中求得AC的长即可求得
DF,结合DF=DC+CF=DC+AD=6即可求得BD的长,在Rt△ABC中求得AC的长即可求得![]() 的值;
的值;
(3)当BD=CD时,如图3中,过点B作MN∥DC,过点C作CN⊥MN,垂足为N,延长DA交MN于点M,易得四边形DCNM是矩形,△ABM∽△BCN,从而可得![]() ,设AM=6y,BN=8y,BM=6x,CN=8x,则易得BD=10x,由BD=DC=MN=MB+BN可得10x=6x+8y,则x=2y,由此在Rt△ABM中,可得AB=
,设AM=6y,BN=8y,BM=6x,CN=8x,则易得BD=10x,由BD=DC=MN=MB+BN可得10x=6x+8y,则x=2y,由此在Rt△ABM中,可得AB=![]() =6
=6![]() y,结合(1)中所得∠BCD=∠MAB即可由sin∠MAB=
y,结合(1)中所得∠BCD=∠MAB即可由sin∠MAB=![]() 求得sin∠BCD的值了.
求得sin∠BCD的值了.
详解:
(1)如图1中,过点B作AD的垂线BE交DA的延长线于点E,
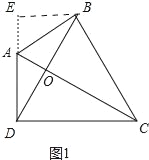
∵∠ABC=∠ADC=90°,
∴∠ADC+∠ABC=180°,
∴点A、B、C、D四点共圆,
∴∠BDE=∠ACB,∠EAB=∠BCD,
∵∠BED=∠ABC=90°,
∴△BED∽△ABC,
∴![]() ,
,
∵ ∠EAB=∠BCD,sin∠EAB=![]() ,
,
∴sin∠BCD=![]() ;
;
(2)如图2中,过点B作BF⊥BD交DC的延长线于F.
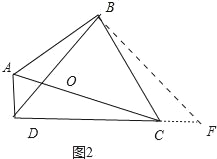
∵∠ABC=∠DBF=90°,∠BAD+∠BCD+∠ABC+∠ADC=360°,∠ABC+∠ADC=180°,
∴∠BAD=180°﹣∠BCD=∠BCF,
∵∠BCF=∠BAD,BC=BA,
∴△DAB≌△CBF,
∴BD=BF,AD=CF,
∵∠DBF=90°,
∴△BDF是等腰直角三角形,
∴BD=![]() DF,
DF,
∵AD+CD=6,
∴CF+CD=DF=6,
∴BD=3![]() ,AC=
,AC=![]() ,
,
∴![]() .
.
(3)当BD=CD时,如图3中,过点B作MN∥DC,过点C作CN⊥MN,垂足为N,延长DA交MN于点M,则四边形DCNM是矩形,△ABM∽△BCN,
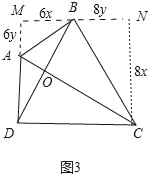
∴![]() ,
,
设AM=6y,BN=8y,BM=6x,CN=8x,
在Rt△BDM中,BD=![]() =10x,
=10x,
∵BD=DC,
∴10x=6x+8y,
∴x=2y,
在Rt△ABM中,AB=![]() =6
=6![]() y,
y,
∴sin∠BCD=sin∠MAB=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=﹣2x﹣1经过抛物线上一点B(﹣2,m),且与y轴、直线x=2分别交于点D、E.
(1)求m的值及该抛物线对应的函数关系式;
(2)求证:①CB=CE;②D是BE的中点;
(3)若P(x,y)是该抛物线上的一个动点,是否存在这样的点P,使得PB=PE?若存在,试求出所有符合条件的点P的坐标;若不存在,请说明理由.
![]()
![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两组卡片共5张,A组的三张分别写有数字2,4,6,B组的两张分别写有3,5.它们除了数字外没有任何区别,
(1)随机从A组抽取一张,求抽到数字为2的概率;
(2)随机地分别从A组、B组各抽取一张,请你用列表或画树状图的方法表示所有等可能的结果.现制定这样一个游戏规则:若选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市在“十一”长假期间对顾客实行优惠,规定如下:
一次性购物金额 | 优惠办法 |
不超过100元 | 不予优惠 |
超过100元但不超过500元 | 超过100元部分给予九折优惠 |
超过500元 | 超过500元部分给予八折优惠 |
(1)小明的爷爷一次性购200元的保健食品,他实际付款_____元;小明妈妈一次性购300元的衣服,她实际付款_____元;如果他们两人合作付款,则能少付_____元;
(2)小芳奶奶在该超市一次性购物x元生活用品,当x大于或等于500时,她实际付款_____元;(用含x的式子表示,写最简结果)
(3)如果小芳奶奶两次购物货款合计900元,第一次购物的货款为a元(![]() ),两次购物小芳奶奶实际付款多少元?(用含a的式子表示)
),两次购物小芳奶奶实际付款多少元?(用含a的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
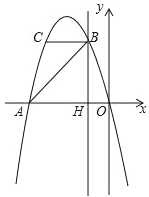
【题目】如图,抛物线y=ax2+bx过A(﹣4,0),B(﹣1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.
(1)求抛物线的函数表达式;
(2)写出点C的坐标,并求出△ABC的面积;
(3)点P是抛物线上一动点,且位于x轴的下方,当△ABP的面积为15时,求出点P的坐标;
(4)若点M在直线BH上运动,点N在x轴上运动,当以点C、M、N为顶点的三角形为等腰直角三角形时,请直接写出此时点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过A(3,0),B(0,3)两点.
经过A(3,0),B(0,3)两点.
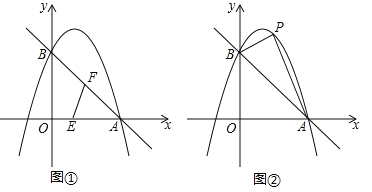
(1)求此抛物线的解析式和直线AB的解析式;
(2)如图①,动点E从O点出发,沿着OA方向以1个单位/秒的速度向终点A匀速运动,同时,动点F从A点出发,沿着AB方向以![]() 个单位/秒的速度向终点B匀速运动,当E,F中任意一点到达终点时另一点也随之停止运动,连接EF,设运动时间为t秒,当t为何值时,△AEF为直角三角形?
个单位/秒的速度向终点B匀速运动,当E,F中任意一点到达终点时另一点也随之停止运动,连接EF,设运动时间为t秒,当t为何值时,△AEF为直角三角形?
(3)如图②,取一根橡皮筋,两端点分别固定在A,B处,用铅笔拉着这根橡皮筋使笔尖P在直线AB上方的抛物线上移动,动点P与A,B两点构成无数个三角形,在这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时点P的坐标;如果不存在,请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,现同时将点
,现同时将点![]() ,
,![]() 分别向上平移2个单位,再向右平移1个单位,分别得到点
分别向上平移2个单位,再向右平移1个单位,分别得到点![]() ,
,![]() 的对应点
的对应点![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
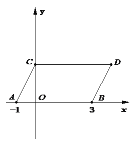
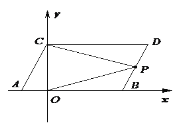
(1)求点![]() ,
,![]() 的坐标及四边形
的坐标及四边形![]() 的面积
的面积![]()
(2)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,连接
,连接![]() ,
,![]() ,使
,使![]() ,若存在这样一点,求出点
,若存在这样一点,求出点![]() 的坐标,若不存在,试说明理由.
的坐标,若不存在,试说明理由.
(3)点![]() 是线段
是线段![]() 上的一个动点,连接
上的一个动点,连接![]() ,
,![]() ,当点
,当点![]() 在
在![]() 上移动时(不与
上移动时(不与![]() ,
,![]() 重合)给出下列结论:
重合)给出下列结论:
①![]() 的值不变,②
的值不变,② ![]() 的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学七年级同学到野外开展数学综合实践活动,在营地看到一池塘,同学们想知道池塘两端的距离.有一位同学设计了如下测量方案:先在平地上取一个可直接到达A、B的点E(A、B为池塘的两端),连接AE、BE并分别延长AE至D,BE至C,使ED=AE,EC=EB,测出CD的长作为AB之间的距离.
(1)他的方案可行吗?请说明理由.
(2)若测得CD=10m,则池塘两端的距离是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com