
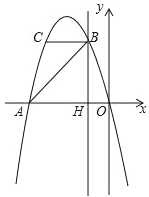
����Ŀ����ͼ��������y=ax2+bx��A����4��0����B����1��3�����㣬��C��B���������ߵĶԳ���Գƣ�����B��ֱ��BH��x�ᣬ��x���ڵ�H��
��1���������ߵĺ�������ʽ��
��2��д����C�����꣬�������ABC�������
��3����P����������һ���㣬��λ��x����·�������ABP�����Ϊ15ʱ�������P�����ꣻ
��4������M��ֱ��BH���˶�����N��x�����˶������Ե�C��M��NΪ�����������Ϊ����ֱ��������ʱ����ֱ��д����ʱ��N�����꣮
 ��������
��������
���𰸡���1��y=��x2��4x����2��3����3����P����Ϊ����6����12����1����5������4��N������Ϊ��2��0����4��0����2��0����4��0����
��������������
��1������A��B���������y=ax2+bx���г�����a��b�ķ����飬�ⷽ�������a��b��ֵ���ɵõ������ߵĽ���ʽy=��x2��4x��
��2������1���������ߵĽ���ʽ��Ϊ������ʽ���õ������ߵĶԳ��ᣬ��ϵ�B�����꼴����õ�C�����꣬������A��B��C��������꼴�����S��ABC��ֵ��
��3������ͼ1������P��PF��ֱx�ᣬ��ֱ��AB�ڵ�F������A��B���������ֱ��AB�Ľ���ʽy=x+4�����P�ĺ�����Ϊm������P������Ϊ��m����m2��4m������F������Ϊ��m��m+4�����ɴ˿ɵ�PF= m2+5m+4��Ȼ����S��PAB=S��PFB-S��PFA=15�ɵ���![]() ����m2+5m+4����[(-1-m)-(-4-m)]=15����˷������m��ֵ���ɵõ���P�����ꣻ
����m2+5m+4����[(-1-m)-(-4-m)]=15����˷������m��ֵ���ɵõ���P�����ꣻ
��4�����Ե�C��M��NΪ�����������Ϊ����ֱ��������ʱ���ֵ�C��M��N�ֱ�Ϊֱ�Ƕ�����������������ۣ�I����MΪֱ�Ƕ��㣬��M��x���Ϸ�����MΪֱ�Ƕ�������M��x����·���II����NΪֱ�Ƕ�������N��y����Ҳࣻ��NΪֱ�Ƕ�������N��y�����ࣻIII��CΪֱ�Ƕ��㣻�����������������Ӧ��ͼ�Σ��ٽ����֪�������з������.
��⣺
��1���ѵ�A����4��0����B����1��3������������y=ax2+bx�У�
��![]() �����
�����![]() ��
��
�������߱���ʽΪy=��x2��4x��
��2����y=��x2+4x=����x+2��2+4��
�������߶Գ���Ϊx=��2��
����C�͵�B���ڶԳ���Գƣ���B������Ϊ����1��3����
��C����3��3����
��BC=2��
��S��ABC=![]() ��2��3=3��
��2��3=3��
��3����ͼ1����P����PF��ֱx�ᣬ��ֱ��AB�ڵ�F��
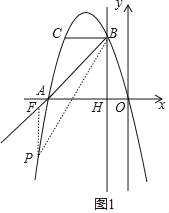
��A����4��0����B����1��3����
��ֱ��AB�Ľ���ʽΪy=kx+b��
��![]() �����
�����![]() ��
��
��ֱ��AB�Ľ���ʽΪy=x+4��
���P��m����m2��4m������F��m��m+4����
��PF=m+4+m2+4m=m2+5m+4��
��S��PAB=![]() ����m2+5m+4����3=15��
����m2+5m+4����3=15��
m2+5m��6=0��
���m1=��6��m2=1��
����P��������6����12����1����5����
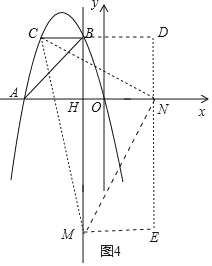
��4���Ե�C��M��NΪ�����������Ϊ����ֱ��������ʱ��������������ۣ�
���Ե�MΪֱ�Ƕ�����M��x���Ϸ�ʱ����ͼ2��CM=MN����CMN=90�㣬
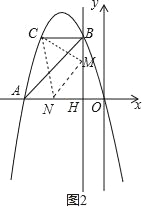
����CBM�ա�MHN��
��BC=MH=2��BM=HN=3��2=1��
��ON=OH+NH=2��
��N����2��0����
���Ե�MΪֱ�Ƕ�����M��x���·�ʱ����ͼ3��

�������ߣ�������ͼ��ʾ����ֱ�������Σ�Rt��NEM��Rt��MDC��
��Rt��NEM��Rt��MDC��
��EM=CD=5��
��OH=1��
��ON=NH��OH=5��1=4��
��N��4��0����
���Ե�NΪֱ�Ƕ�����N��y���Ҳ�ʱ����ͼ4��CN=MN����MNC=90�����������ߣ�
ͬ����Rt��NEM��Rt��MDC��
��ME=NH=DN=3��
��ON=3��1=2��
��N��2��0����
���Ե�NΪֱ�Ƕ�����N��y�����ʱ���������ߣ���ͼ5��
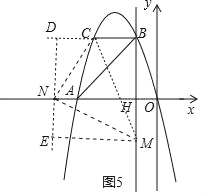
ͬ����ME=DN=NH=3��
��ON=1+3=4��
��N����4��0����
����CΪֱ�Ƕ���ʱ�����ڵ�C��-3��3����x��ľ���͵������߶Գ���x=-2�ľ��벻��ȣ����Դ�ʱ���ܹ������������ĵ���ֱ�������Σ�
���Ͽ�֪����CMNΪ����ֱ��������ʱN������Ϊ��2��0����4��0����2��0����4��0����


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�ǵȱߡ�ABC��һ�㣬��AOB=110�㣬��BOC=a������BOC�Ƶ�C��˳ʱ�뷽����ת60��á�ADC������OD��

��1����֤����COD�ǵȱ������Σ�
��2����a=150��ʱ�����жϡ�AOD����״����˵�����ɣ�
��3��̽������aΪ���ٶ�ʱ����AOD�ǵ��������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABCD�У��Խ���AC��BD�ཻ��O��EF����O������AF��CE��
��1����֤����BFO�ա�DEO��
��2����AF��BC�����ж��ı���AFCE����״��������֤����
��3�����ڣ�2����������������EFƽ�֡�AEC�����ж��ı���AFCE����״������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ�����ֲ�ͬ�ͺŵ��·�����֪����A���ͺ��·�9����B���ͺ��·�10��������1810Ԫ��������A���ͺ��·�12����B���ͺ��·�8��������1880Ԫ����֪����һ��A�ͺ��·��ɻ���18Ԫ������һ��B�ͺ��·��ɻ���30Ԫ��Ҫʹ����������л���������699Ԫ����A�ͺ��·�������28����
��1����A��B�ͺ��·����۸��Ƕ���Ԫ��
��2������֪����A�ͺ��·���B�ͺ��·���2������4�������̵�����ν����п��м��ַ�������������������
���𰸡���1��A���ͺŵ��·�ÿ��90Ԫ��B���ͺŵ��·�100Ԫ����2�������ֽ������������������.
�������������������1��������ϵΪ��A���ͺ��·�9��������+B���ͺ��·�10��������=1810��A���ͺ��·�12��������+B���ͺ��·�8��������=1880��
��2���ؼ��������ǣ�����������699Ԫ����A�ͺ��·�������28������ϵʽΪ��18��A�ͼ���+30��B�ͼ�����699��A�ͺ��·�������28��
�����������1����A���ͺŵ��·�ÿ��xԪ��B���ͺŵ��·�yԪ��
��![]() ��
��
��֮��![]() .
.
��A���ͺŵ��·�ÿ��90Ԫ��B���ͺŵ��·�100Ԫ��
��2����B�ͺ��·�����m��,��A�ͺ��·�����(2m+4)����
�ɵã�![]() ��
��
��֮��192m12��
��m��������
��m=10��11��12��2m+4=24��26��28.
�������ֽ���������
(1)B�ͺ��·�����10����A�ͺ��·�����24����
(2)B�ͺ��·�����11����A�ͺ��·�����26����
(3)B�ͺ��·�����12����A�ͺ��·�����28����
�㾦���㾦��������Ҫ�����Ԫһ�η������һԪһ�β���ʽ���ʵ�������Ӧ�ã�����Ĺؼ��Ƕ�����Ŀ����˼��������Ŀ���������������δ֪�����ֱ��ҳ�����������Ӧ�Ĺ���ʱ�䣬�ҳ����ʵĵ�����ϵ���г������飬�����.
�����͡������
��������
21
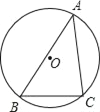
����Ŀ����ͼ�������ABC�ڽ�����O������O�İ뾶Ϊ6��sinA=![]() ����BC�ij���
����BC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��0��4����ֱ������ϵy����һ�㣬����P��ԭ��O��������x���������˶����ٶ�Ϊÿ��1����λ���ȣ���PΪֱ�Ƕ����ڵ�һ������������Rt��APB����P����˶�ʱ��Ϊt�룮
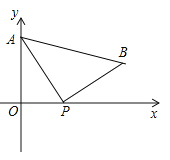
��1����AB//x�ᣬ��t��ֵ��
��2����t=3ʱ������ƽ������һ��M������A�غϣ���ʹ����M��P��BΪ����������κ͡�ABPȫ�ȣ��������M�����ꣻ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
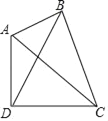
����Ŀ����ͼ���ı���ABCD�У�AC��BD�����ĶԽ��ߣ���ABC=��ADC=90�㣬��BCD����ǣ�
��1����BD=BC��֤����sin��BCD=![]() ��
��
��2����AB=BC=4��AD+CD=6����![]() ��ֵ��
��ֵ��
��3����BD=CD��AB=6��BC=8����sin��BCD��ֵ��
��ע������ɸ�����Ҫ�Լ���ͼ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() �뷴��������
�뷴��������![]() ��ͼ���ڵ�һ������һ�������㣬�������Ϊ1����һ�κ���
��ͼ���ڵ�һ������һ�������㣬�������Ϊ1����һ�κ���![]() ��ͼ������ǣ� ��
��ͼ������ǣ� ��
A. 
B. 
C. 
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���A��110�㣬E��F�ֱ��DZ�AB��BC���е㣬EP��CD�ڵ�P�����FPC����������
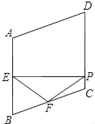
A. 35��B. 45��C. 50��D. 55��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
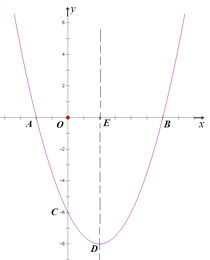
����Ŀ�������ģ���ͼ��������![]() ��x�ύ��A��B���㣬��y�ύ�ڵ�C����Գ��ύ�������ڵ�D����x���ڵ�E����֪OB=OC=6.
��x�ύ��A��B���㣬��y�ύ�ڵ�C����Գ��ύ�������ڵ�D����x���ڵ�E����֪OB=OC=6.
��1���������ߵĽ���ʽ����D�����ꣻ
��2������BD��FΪ��������һ���㣬����FAB=��EDBʱ�����F�����ꣻ
��3��ƽ����x���ֱ�߽���������M��N���㣬���߶�MNΪ�Խ���������MPNQ������P��x���ϣ���PQ=![]() MNʱ�������ζԽ���MN�ij�.
MNʱ�������ζԽ���MN�ij�.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com