
【题目】如图,A(0,4)是直角坐标系y轴上一点,动点P从原点O出发,沿x轴正半轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒.
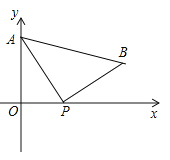
(1)若AB//x轴,求t的值;
(2)当t=3时,坐标平面内有一点M(不与A重合),使得以M、P、B为顶点的三角形和△ABP全等,请求出点M的坐标;
【答案】(1)4;(2) (4,7)或(10,-1)或(6,-4)或(0,4).
【解析】
(1)由AB∥x轴,可找出四边形ABCO为长方形,再根据△APB为等腰三角形可得知∠OAP=45°,从而得出△AOP为等腰直角三角形,由此得出结论;
(2)由全等三角形的性质和等腰三角形的性质可得出结论,注意分类讨论.
解:(1)过点B作BC⊥x轴于点C,如图所示.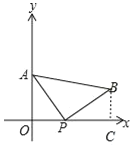
∵AO⊥x轴,BC⊥x轴,且AB∥x轴,
∴四边形ABCO为长方形,
∴AO=BC=4.
∵△APB为等腰直角三角形,
∴AP=BP,∠PAB=∠PBA=45°,
∴∠OAP=90°-∠PAB=45°,
∴△AOP为等腰直角三角形,
∴OA=OP=4.
∴t=4÷1=4(秒),
故t的值为4.
(2)当t=3时,OP=3.
∵OA=4,
∴由勾股定理,得
AP=![]() =5.
=5.
∴AP=PB=5,AB=5![]() ,
,
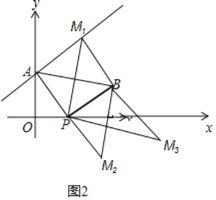
∴当△MPB≌△ABP时,此时四边形APBM1是正方形,四边形APBM3是平行四边形,易得M1(4,7)、M3(10,-1);
当△MPB≌△APB时,此时点M2与点A关于点P对称,易得M2(6,-4).
当两个三角形重合时,此时符合条件的点M的坐标是(0,4);
综上所述,点M的坐标为(4,7)或(10,-1)或(6,-4)或(0,4);


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:
【题目】为传播“绿色出行,低碳生活”的理念,小贾同学的爸爸从家里出发,骑自行车去图书馆看书,图1表达的是小贾的爸爸行驶的路程![]() (米)与行驶时间
(米)与行驶时间![]() (分钟)的变化关系
(分钟)的变化关系
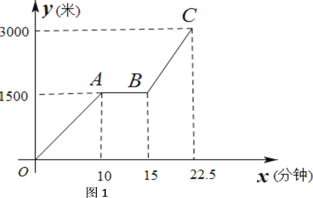
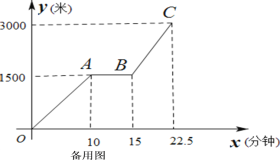
(1)求线段BC所表达的函数关系式;
(2)如果小贾与爸爸同时从家里出发,小贾始终以速度120米/分钟行驶,当小贾与爸爸相距100米是,求小贾的行驶时间;
(3)如果小贾的行驶速度是![]() 米/分,且在途中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出
米/分,且在途中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富老年人的晚年生活,甲、乙两单位准备组织退休职工到某风景区游玩.甲、乙两单位退休职工共![]() 人,其中乙单位人数少于
人,其中乙单位人数少于![]() 人,且甲单位人数不够
人,且甲单位人数不够![]() 人.经了解,该风景区的门票价格如下表:
人.经了解,该风景区的门票价格如下表:
数量(张) |
|
|
|
单价(元/张) |
|
|
|
如果两单位分别单独购买门票,一共应付![]() 元.
元.
(1)甲、乙两单位各有多少名退休职工准备参加游玩?
(2)如果甲单位有![]() 名退休职工因身体原因不能外出游玩,那么你有几种购买方案,通过比较,你该如何购买门票才能最省钱?
名退休职工因身体原因不能外出游玩,那么你有几种购买方案,通过比较,你该如何购买门票才能最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场第一次用11000元购进某款拼装机器人进行销售,很快销售一空,商家又用24000元第二次购进同款机器人,所购进数量是第一次的2倍,但单价贵了10元.
(1)求该商家第一次购进机器人多少个?
(2)若所有机器人都按相同的标价销售,要求全部销售完毕的利润率不低于20%(不考虑其它因素),那么每个机器人的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前“微信”、“支付宝”、“共享单车”和“网购”给我们带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行了调查,随机调查了![]() 人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.

(1)根据图中信息求出![]() =___________,
=___________,![]() =_____________;
=_____________;
(2)请你帮助他们将这两个统计图补全;
(3)根据抽样调查的结果,请估算全校2000名学生种,大约有多少人最认可“微信”这一新生事物?
查看答案和解析>>
科目:初中数学 来源: 题型:
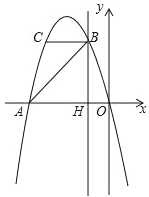
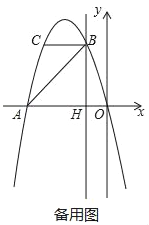
【题目】如图,抛物线y=ax2+bx过A(﹣4,0),B(﹣1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.
(1)求抛物线的函数表达式;
(2)写出点C的坐标,并求出△ABC的面积;
(3)点P是抛物线上一动点,且位于x轴的下方,当△ABP的面积为15时,求出点P的坐标;
(4)若点M在直线BH上运动,点N在x轴上运动,当以点C、M、N为顶点的三角形为等腰直角三角形时,请直接写出此时点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆出租车从A地出发,在一条东西走向的街道上往返,每次行驶的路程(记向东为正)记录如下(x>6且x<14,单位:km):

(1)写出这辆出租车每次行驶的方向;
(2)求经过连续4次行驶后,这辆出租车所在的位置(结果可用x表示);
(3)这辆出租车一共行驶了多少路程(结果用x表示)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 ,∠E=∠F=90°,∠B=∠C,AC=AB,给出下列结论:① ∠1=∠2;② BE=CF;③ △ACN≌△ABM;④ CD=DN,其中正确的结论有( )个

A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com