
����Ŀ��Ŀǰ����������֧�����������������������������������Ǵ����˺ܶ������������ѧС����У�ڶ��������Ͽɵ��Ĵ����������������˵��飬���������![]() �ˣ�ÿ��ѧ����ѡһ����ֻ�ܴ���������ѡ��һ�֣��������������Ƴ����²�������ͳ��ͼ��
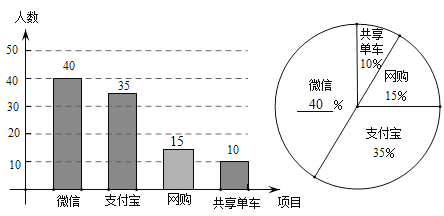
�ˣ�ÿ��ѧ����ѡһ����ֻ�ܴ���������ѡ��һ�֣��������������Ƴ����²�������ͳ��ͼ��

��1������ͼ����Ϣ���![]() =___________��
=___________��![]() =_____________��
=_____________��
��2������������ǽ�������ͳ��ͼ��ȫ��
��3�����ݳ�������Ľ���������ȫУ2000��ѧ���֣���Լ�ж��������Ͽ���������һ�������
���𰸡���1��100��35����2�������������3��800�ˣ�
��������
��1���ɹ��������������Լ�����ռ�ٷֱȿ����������m����֧�������������������ɵ���ٷֱ�n��ֵ��
��2�����������������İٷֱȿ�������������������������������������ٷֱȣ��ɴ˼��ɲ�ȫ����ͼ�Σ�
��3��������������������������ռ�ٷֱȼ�����ô𰸣�
��1������������m=10��10%=100��
֧������������ռ�ٷֱ�n%=![]() =35%������n=35��
=35%������n=35��
�ʴ�Ϊ��100��35��
��2����������Ϊ��100��15%=15�ˣ�
�Ŷ�Ӧ�İٷֱ�Ϊ��![]() ��
��
��ȫͼ����ͼ��ʾ��
��3������ȫУ2000��ѧ���֣����Ͽ���������һ�������������Ϊ��2000��40%=800�ˣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���С½�� A �س����������г���ͬһ��·��ʻ�� B �أ�����������صľ��� s����ʻʱ��t֮��Ĺ�ϵ��ͼ����ͼ������ͼ��ش��������⣺
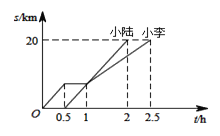
(1) С����;�ж�����ʱ��Ϊ___________h��С½�� A �ص� B �ص��ٶ���________km/h��
(2) ��С���С½����ʱ�������� B �ص�·����____________ǧ�ף�
(3) д��С���ڶ���֮ǰ�� A �ص�·��s����ʻʱ��t֮��ĺ�����ϵʽΪ_____________________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ�ٰ������簲ȫ֪ʶ���⾺�������ߡ����꼶���ݳ����ɼ���ѡ��5��ѡ����ɴ����ӲμӾ����������Ӹ�ѡ����5��ѡ�ֵľ����ɼ���ͼ��ʾ��
ƽ���֣��֣� | ��λ�����֣� | �������֣� | �����2�� | |
���꼶 | a | 85 | b | S���꼶2 |
���꼶 | 85 | c | 100 | 160 |
��1������ͼʾ��գ�a���� ����b���� ����c���� ����
��2��������ӳɼ���ƽ��������λ�����з������ĸ������ӵľ����ɼ��Ϻã�
��3���������꼶�����Ӿ����ɼ��ķ���S���꼶2�����ж���һ��������ѡ�ֳɼ���Ϊ�ȶ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���������ABC�У���ABC=45�㣬����AD��BE�ཻ�ڵ�F��
��1���ж�BF��AC��������ϵ��˵�����ɣ�
��2����ͼ2������ACD���߶�AD���ۣ���C����BD�ϵĵ�M��AM��BE�ཻ�ڵ�N����DE��AMʱ���ж�NE��AC��������ϵ��˵�����ɣ�
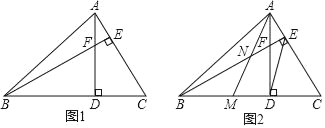
���𰸡���1��BF=AC�����ɼ���������2��NE=![]() AC�����ɼ�����.
AC�����ɼ�����.
�������������������1����ͼ1��֤����ADC�ա�BDF��AAS�����ɵ�BF=AC��
��2����ͼ2�����۵��ã�MD=DC���ȸ�����������λ�ߵ����ۿɵã�AE=EC�����߶δ�ֱƽ���ߵ����ʵã�AB=BC�����ABE=��CBE����ϣ�1���ã���BDF�ա�ADM�����DBF=��MAD�����֤����ANE=��NAE=45�㣬��AE=EN������EN=![]() AC��
AC��
���������
��1��BF=AC�������ǣ�
��ͼ1����AD��BC��BE��AC��
���ADB=��AEF=90����
�ߡ�ABC=45����
���ABD�ǵ���ֱ�������Σ�
��AD=BD��
�ߡ�AFE=��BFD��
���DAC=��EBC��
����ADC����BDF��
��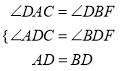 ��
��
���ADC�ա�BDF��AAS����
��BF=AC��
��2��NE=![]() AC�������ǣ�
AC�������ǣ�
��ͼ2�����۵��ã�MD=DC��
��DE��AM��
��AE=EC��
��BE��AC��
��AB=BC��
���ABE=��CBE��
�ɣ�1���ã���ADC�ա�BDF��
�ߡ�ADC�ա�ADM��
���BDF�ա�ADM��
���DBF=��MAD��
�ߡ�DBA=��BAD=45����
���DBA����DBF=��BAD����MAD��
����ABE=��BAN��
�ߡ�ANE=��ABE+��BAN=2��ABE��
��NAE=2��NAD=2��CBE��
���ANE=��NAE=45����
��AE=EN��
��EN=![]() AC��
AC��
�����͡������
��������
19
����Ŀ��ijУѧ�������������ѧ���������ѡ��һ�����µ�ѧ������ϯ���Լס��ҡ���������ѡ�˽����˱��Ժ����ԣ����˵IJ��Գɼ����±���ʾ��
������Ŀ | ���Գɼ�/�� | ||
�� | �� | �� | |
���� | 75 | 80 | 90 |
���� | 93 | 70 | 68 |
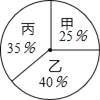
����¼�ó���ѧУ��֯200��ѧ������ͶƱ�Ƽ��ķ�ʽ�������˽����������������˵�Ʊ��������ͳ��ͼ��ʾ��û����Ȩ��ÿλͬѧֻ���Ƽ�1�ˣ���ÿ��1Ʊ��1����
��1���ֱ����������������ĵ÷֣�
��2������ʵ����Ҫ��ѧУ�����ԡ����ԡ�������������÷ְ�3��3��4�ı���ȷ�����˳ɼ���������˭�ᵱѡѧ������ϯ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�������ֳ��������Ͻ���֪����ij�����y�ף�����Ŀ�����x�ף���һ�û��裨1���͵Ĵ���2������2���͵Ĵ���2��.
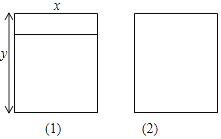
(1)�ú�x��y��ʽ�ӱ�ʾ�������Ͻ�ij��ȣ�
(2)��1m���Ͻ��ƽ������Ϊ100Ԫ����x=1.2��y=1.5ʱ�����Ͻ���ܷ���Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��0��4����ֱ������ϵy����һ�㣬����P��ԭ��O��������x���������˶����ٶ�Ϊÿ��1����λ���ȣ���PΪֱ�Ƕ����ڵ�һ������������Rt��APB����P����˶�ʱ��Ϊt�룮
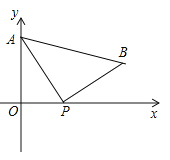
��1����AB//x�ᣬ��t��ֵ��
��2����t=3ʱ������ƽ������һ��M������A�غϣ���ʹ����M��P��BΪ����������κ͡�ABPȫ�ȣ��������M�����ꣻ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1����ƽ��ֱ������ϵ�У���A��B�ֱ���x��y���ϣ���B������Ϊ��0��1������BAO=30�㣮

��1����AB�ij��ȣ�
��2����ABΪһ�����ȱߡ�ABE����OA�Ĵ�ֱƽ����MN��AB�Ĵ���AD�ڵ�,��֤��BD=OE��
��3���ڣ�2���������£�����DE��AB��F,��֤��FΪDE���е㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���ֱ֪��![]() ��x�ᡢy��ֱ���A��B���㣬��C��y����һ��
��x�ᡢy��ֱ���A��B���㣬��C��y����һ��![]() ������ƽ����ֱ��AC�۵���ʹ��B�պ�����x�������ϣ����C������Ϊ
������ƽ����ֱ��AC�۵���ʹ��B�պ�����x�������ϣ����C������Ϊ![]() ����
����![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
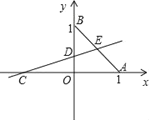
����Ŀ����֪����ͼ��ƽ��ֱ������ϵxOy�У�B��0��1����OB��OC��OA��A��C�ֱ���x������������ϣ�����C��ֱ���Ƶ�C��ת����y���ڵ�D�����߶�AB�ڵ�E��
��1�����OAB�Ķ�����ֱ��AB�Ľ���ʽ��
��2������OCD���BDE�������ȣ����D�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com