
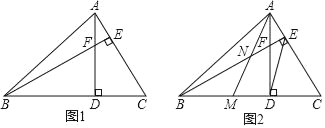
����Ŀ����ͼ1���������ABC�У���ABC=45�㣬����AD��BE�ཻ�ڵ�F��
��1���ж�BF��AC��������ϵ��˵�����ɣ�
��2����ͼ2������ACD���߶�AD���ۣ���C����BD�ϵĵ�M��AM��BE�ཻ�ڵ�N����DE��AMʱ���ж�NE��AC��������ϵ��˵�����ɣ�
���𰸡���1��BF=AC�����ɼ���������2��NE=![]() AC�����ɼ�����.
AC�����ɼ�����.
�������������������1����ͼ1��֤����ADC�ա�BDF��AAS�����ɵ�BF=AC��
��2����ͼ2�����۵��ã�MD=DC���ȸ�����������λ�ߵ����ۿɵã�AE=EC�����߶δ�ֱƽ���ߵ����ʵã�AB=BC�����ABE=��CBE����ϣ�1���ã���BDF�ա�ADM�����DBF=��MAD�����֤����ANE=��NAE=45�㣬��AE=EN������EN=![]() AC��
AC��
���������
��1��BF=AC�������ǣ�
��ͼ1����AD��BC��BE��AC��
���ADB=��AEF=90����
�ߡ�ABC=45����
���ABD�ǵ���ֱ�������Σ�
��AD=BD��
�ߡ�AFE=��BFD��
���DAC=��EBC��
����ADC����BDF��
��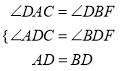 ��
��
���ADC�ա�BDF��AAS����
��BF=AC��
��2��NE=![]() AC�������ǣ�
AC�������ǣ�
��ͼ2�����۵��ã�MD=DC��
��DE��AM��
��AE=EC��
��BE��AC��
��AB=BC��
���ABE=��CBE��
�ɣ�1���ã���ADC�ա�BDF��
�ߡ�ADC�ա�ADM��
���BDF�ա�ADM��
���DBF=��MAD��
�ߡ�DBA=��BAD=45����
���DBA����DBF=��BAD����MAD��
����ABE=��BAN��
�ߡ�ANE=��ABE+��BAN=2��ABE��
��NAE=2��NAD=2��CBE��
���ANE=��NAE=45����
��AE=EN��
��EN=![]() AC��
AC��
�����͡������
��������
19
����Ŀ��ijУѧ�������������ѧ���������ѡ��һ�����µ�ѧ������ϯ���Լס��ҡ���������ѡ�˽����˱��Ժ����ԣ����˵IJ��Գɼ����±���ʾ��
������Ŀ | ���Գɼ�/�� | ||
�� | �� | �� | |
���� | 75 | 80 | 90 |
���� | 93 | 70 | 68 |
����¼�ó���ѧУ��֯200��ѧ������ͶƱ�Ƽ��ķ�ʽ�������˽����������������˵�Ʊ��������ͳ��ͼ��ʾ��û����Ȩ��ÿλͬѧֻ���Ƽ�1�ˣ���ÿ��1Ʊ��1����
��1���ֱ����������������ĵ÷֣�
��2������ʵ����Ҫ��ѧУ�����ԡ����ԡ�������������÷ְ�3��3��4�ı���ȷ�����˳ɼ���������˭�ᵱѡѧ������ϯ��
���𰸡���1���÷�50�֣��ҵ÷�80�֣����÷�70�֣���2���ҵ�ѡѧ������ϯ��
�������������������1������������Էֱ���ü��ұ����˵���������÷֣�
��2������������Էֱ���ü��ұ����˵����ճɼ���Ȼ��Ƚϴ�С���ɽ���⣮
���������(1)������ɵã�
����������ĵ÷��ǣ�200��25%=50(��)��
����������ĵ÷��ǣ�200��40%=80(��)��
����������ĵ÷��ǣ�200��35%=70(��)��
(2)������ɵã�
�ijɼ��ǣ� ![]() (��)��
(��)��
�ҵijɼ��ǣ� ![]() (��)��
(��)��
���ijɼ��ǣ� ![]() (��)��
(��)��
��70.4<73.9<77��
���ҵ�ѡѧ������ϯ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����ij�µ�������Ȧ�����ڵ��ĸ�����������ĸ����ֵĺ�Ϊ![]() ����ô���ĸ�����������λ�õ���ʽ�ǣ� ��
����ô���ĸ�����������λ�õ���ʽ�ǣ� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ��һ���ı��εĿյ�ABCD����ͼ��ʾ����������A=90�㣬AB=6m��BC=24m��CD=26m��DA=8m.
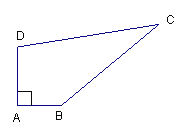
��1�����ı���ABCD�������
��2��ѧУ�ƻ��ڿյ�����ֲ��Ƥ����ÿƽ���ײ�Ƥ��Ҫ200Ԫ����ѧУ��ҪͶ������ʽ����Ƥ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˷ḻ�����˵���������ס�������λ����֯����ְ����ij�羰������.�ס�������λ����ְ����![]() �ˣ������ҵ�λ��������
�ˣ������ҵ�λ��������![]() �ˣ��Ҽ�λ��������
�ˣ��Ҽ�λ��������![]() ��.���˽⣬�÷羰������Ʊ�۸����±�:
��.���˽⣬�÷羰������Ʊ�۸����±�:
����(��) |
|
|
|
����(Ԫ/��) |
|
|
|
�������λ�ֱ�������Ʊ��һ��Ӧ��![]() Ԫ.
Ԫ.
��1���ס�������λ���ж���������ְ�����μ����棿
��2�������λ��![]() ������ְ��������ԭ����������棬��ô���м��ֹ�����ͨ���Ƚϣ������ι�����Ʊ������ʡǮ��
������ְ��������ԭ����������棬��ô���м��ֹ�����ͨ���Ƚϣ������ι�����Ʊ������ʡǮ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=��x2��2x+3��x�ύ�ڵ�A��B������������x�ἰ���Ϸ��IJ��ּ���C1����C1���ڵ�B�����ĶԳƵ�C2��C2��x�ύ����һ��C����C2���ڵ�C�����ĶԳƵ�C3������C1��C3�Ķ��㣬��ͼ����Ӱ���ֵ����Ϊ_____��

���𰸡�32
�������������������������y=��x2��2x+3��x�ύ�ڵ�A��B��
����y=0ʱ������x2��2x+3=0��
���x=��3��x=1��
��A��B������ֱ�Ϊ����3��0������1��0����
AB�ij���Ϊ4��
��C1��C3�������ֶ���ֱ����������߽�x����E��F���㣮
�������ĶԳƵ����ʣ�x���·����ֿ����ضԳ���ƽ���ֳ������ֲ���C1��C2��
��ͼ��ʾ����Ӱ����ת��Ϊ���Σ�
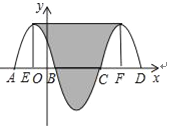
���ݶԳ��ԣ��ɵ�BE=CF=4��2=2����EF=8
�����䷽���ɵ�y=��x2��2x��3=����x+1��2+4
������Ϊ����1��4��������Ӱ���ֵĸ�Ϊ4��
S��=8��4=32��
���㣺��������x��Ľ��㣮
�����͡������
��������
17
����Ŀ���ⷽ�̣���1��2��3x��1��=16����2��![]() ����3��
����3��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳���һ����11000Ԫ����ij��ƴװ�����˽������ۣ��ܿ�����һ�գ��̼�����24000Ԫ�ڶ��ι���ͬ������ˣ������������ǵ�һ�ε�2���������۹���10Ԫ��
��1������̼ҵ�һ�ι��������˶��ٸ���
��2�������л����˶�����ͬ�ı�����ۣ�Ҫ��ȫ��������ϵ������ʲ�����20%���������������أ�����ôÿ�������˵ı�������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ŀǰ����������֧�����������������������������������Ǵ����˺ܶ������������ѧС����У�ڶ��������Ͽɵ��Ĵ����������������˵��飬���������![]() �ˣ�ÿ��ѧ����ѡһ����ֻ�ܴ���������ѡ��һ�֣��������������Ƴ����²�������ͳ��ͼ��
�ˣ�ÿ��ѧ����ѡһ����ֻ�ܴ���������ѡ��һ�֣��������������Ƴ����²�������ͳ��ͼ��

��1������ͼ����Ϣ���![]() =___________��
=___________��![]() =_____________��
=_____________��
��2������������ǽ�������ͳ��ͼ��ȫ��
��3�����ݳ�������Ľ���������ȫУ2000��ѧ���֣���Լ�ж��������Ͽ���������һ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������A�س�������һ����������Ľֵ���������ÿ����ʻ��·�̣�����Ϊ������¼���£�x��6��x��14����λ��km����

��1��д���������ÿ����ʻ�ķ���
��2��������4����ʻ������������ڵ�λ�ã��������x��ʾ����
��3���������һ����ʻ�˶���·�̣������x��ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ�������ڼ䣬ѧУ��ѧ�������黭��Ʒ������ʦ��ȫУ30�����������ȡ��4���ࣨ��A��B��C��D��ʾ����������������Ʒ�����������˷���ͳ�ƣ�������������������ͳ��ͼ��

�����������Ϣ���ش��������⣺
��1������ʦ���õĵ��鷽ʽ�� ����ղ顱�������顱����
��2�����㽫����ͳ��ͼ����������������ȫУ���������ټ���Ʒ��
��3�����ȫУ��������Ʒ����5�����һ�Ƚ���������3��������������2��������Ů������Ҫ�ڻ��һ�Ƚ���������ѡȡ���˲μӱ�����̸�ᣬ�������б�����״ͼ�ķ�������ǡ��ѡȡ������ѧ���Ա���ͬ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com