
【题目】小华在某月的日历上圈出相邻的四个数,算出这四个数字的和为![]() ,那么这四个数在日历上位置的形式是( )
,那么这四个数在日历上位置的形式是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是⊙O的内接四边形,AC为直径,![]() ,DE⊥BC,垂足为E.
,DE⊥BC,垂足为E.

(1)求证:CD平分∠ACE;
(2)判断直线ED与⊙O的位置关系,并说明理由;
(3)若CE=1,AC=4,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知多项式![]() 的常数项式
的常数项式![]() ,次数是
,次数是![]() ,若
,若![]() 两数在数轴上所对应的点为A、B
两数在数轴上所对应的点为A、B
(1)线段AB的长=
(2)数轴上在B点右边有一点C,点C到A、B两点的距离和为11,求点C在数轴上所对应的数;
(3) 若P、Q两点分别从A、B出发,同时沿数轴正方向运动,P点的速度是Q点速度的2倍,且3秒后,2OP=OQ,求点Q运动的速度

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习完一次函数后,小荣遇到过这样的一个新颖的函数:y=|x-1|,小荣根据学校函数的经验,对函数y=|x-1|的图象与性质进行了探究。下面是小荣的探究过程,请补充完成
列表:下表是y与的几组对应值,请补充完整。

(2)描点连线:在平面直角坐标系xOy中,请描出以上表中各对对应值为坐标的点,画出该函数的图象;
(3)进一步探究发现,该函数图象的最低点的坐标是(1,0),结合图数的图象,写出该函数的其他性质(一条即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
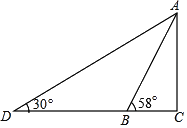
【题目】如图,某游乐园有一个滑梯高度AB,高度AC为3米,倾斜角度为58°.为了改善滑梯AB的安全性能,把倾斜角由58°减至30°,调整后的滑梯AD比原滑梯AB增加多少米?(精确到0.1米)
(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年兴义市加大中职教育投入力度,取得了良好的社会效果。某校随机调查了九年级a名学生升学意向,并根据调查结果绘制如图的两幅不完整的统计图。

请你根据图中信息解答下列问题:
(1)a= ;
(2)扇形统计图中,“职高”对应的扇形的圆心角α= ;
(3)请补全条形统计图;
(4)若该校九年级有学生900名,估计该校共有多少名毕业生的升学意向是职高。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李和小陆从 A 地出发,骑自行车沿同一条路行驶到 B 地,他们离出发地的距离 s和行驶时间t之间的关系的图象如图,根据图象回答下列问题:
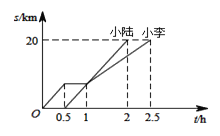
(1) 小李在途中逗留的时间为___________h,小陆从 A 地到 B 地的速度是________km/h;
(2) 当小李和小陆相遇时,他们离 B 地的路程是____________千米;
(3) 写出小李在逗留之前离 A 地的路程s和行驶时间t之间的函数关系式为_____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小都相同.正常水位时,大孔水面宽度AB=20米,顶点M距水面6米(即MO=6米),小孔顶点N距水面4.5米(即NC=4.5米).当水位上涨刚好淹没小孔时,借助图中的直角坐标系,求此时大孔的水面宽度EF.
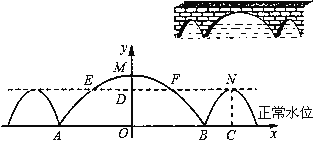
查看答案和解析>>
科目:初中数学 来源: 题型:
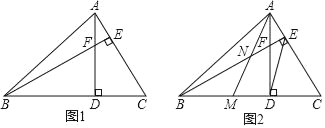
【题目】如图1,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.
(1)判断BF与AC的数量关系并说明理由;
(2)如图2,将△ACD沿线段AD对折,点C落在BD上的点M,AM与BE相交于点N,当DE∥AM时,判断NE与AC的数量关系并说明理由.
【答案】(1)BF=AC,理由见解析;(2)NE=![]() AC,理由见解析.
AC,理由见解析.
【解析】试题分析:(1)如图1,证明△ADC≌△BDF(AAS),可得BF=AC;
(2)如图2,由折叠得:MD=DC,先根据三角形中位线的推论可得:AE=EC,由线段垂直平分线的性质得:AB=BC,则∠ABE=∠CBE,结合(1)得:△BDF≌△ADM,则∠DBF=∠MAD,最后证明∠ANE=∠NAE=45°,得AE=EN,所以EN=![]() AC.
AC.
试题解析:
(1)BF=AC,理由是:
如图1,∵AD⊥BC,BE⊥AC,
∴∠ADB=∠AEF=90°,
∵∠ABC=45°,
∴△ABD是等腰直角三角形,
∴AD=BD,
∵∠AFE=∠BFD,
∴∠DAC=∠EBC,
在△ADC和△BDF中,
∵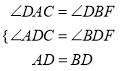 ,
,
∴△ADC≌△BDF(AAS),
∴BF=AC;
(2)NE=![]() AC,理由是:
AC,理由是:
如图2,由折叠得:MD=DC,
∵DE∥AM,
∴AE=EC,
∵BE⊥AC,
∴AB=BC,
∴∠ABE=∠CBE,
由(1)得:△ADC≌△BDF,
∵△ADC≌△ADM,
∴△BDF≌△ADM,
∴∠DBF=∠MAD,
∵∠DBA=∠BAD=45°,
∴∠DBA﹣∠DBF=∠BAD﹣∠MAD,
即∠ABE=∠BAN,
∵∠ANE=∠ABE+∠BAN=2∠ABE,
∠NAE=2∠NAD=2∠CBE,
∴∠ANE=∠NAE=45°,
∴AE=EN,
∴EN=![]() AC.
AC.
【题型】解答题
【结束】
19
【题目】某校学生会决定从三明学生会干事中选拔一名干事当学生会主席,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 75 | 80 | 90 |
面试 | 93 | 70 | 68 |
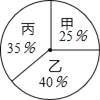
根据录用程序,学校组织200名学生采用投票推荐的方式,对三人进行民主测评,三人得票率如扇形统计图所示(没有弃权,每位同学只能推荐1人),每得1票记1分.
(1)分别计算三人民主评议的得分;
(2)根据实际需要,学校将笔试、面试、民主评议三项得分按3:3:4的比例确定个人成绩,三人中谁会当选学生会主席?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com