
【题目】如图,四边形ABCD是⊙O的内接四边形,AC为直径,![]() ,DE⊥BC,垂足为E.
,DE⊥BC,垂足为E.

(1)求证:CD平分∠ACE;
(2)判断直线ED与⊙O的位置关系,并说明理由;
(3)若CE=1,AC=4,求阴影部分的面积.
【答案】(1)证明见解析;(2)直线ED与⊙O相切.理由见解析.(3)![]() .
.
【解析】
试题分析:(1)根据圆周角定理,由得到![]() ,∠BAD=∠ACD,再根据圆内接四边形的性质得∠DCE=∠BAD,所以∠ACD=∠DCE;
,∠BAD=∠ACD,再根据圆内接四边形的性质得∠DCE=∠BAD,所以∠ACD=∠DCE;
(2)连结OD,如图,利用内错角相等证明OD∥BC,而DE⊥BC,则OD⊥DE,于是根据切线的判定定理可得DE为⊙O的切线;
(3)作OH⊥BC于H,易得四边形ODEH为矩形,所以OD=EH=2,则CH=HE-CE=1,于是有∠HOC=30°,得到∠COD=60°,然后根据扇形面积公式、等边三角形的面积公式和阴影部分的面积=S扇形OCD-S△OCD进行计算.
试题解析:(1)证明:∵![]()
∴∠BAD=∠ACD,
∵∠DCE=∠BAD,
∴∠ACD=∠DCE,
即CD平分∠ACE;
(2)解:直线ED与⊙O相切.理由如下:
连结OD,如图,

∵OC=OD,
∴∠OCD=∠ODC,
而∠OCD=∠DCE,
∴∠DCE=∠ODC,
∴OD∥BC,
∵DE⊥BC,
∴OD⊥DE,
∴DE为⊙O的切线;
(3)解:作OH⊥BC于H,则四边形ODEH为矩形,
∴OD=EH,
∵CE=1,AC=4,
∴OC=OD=2,
∴CH=HE-CE=2-1=1,
在Rt△OHC中,∠HOC=30°,
∴∠COD=60°,
∴阴影部分的面积=S扇形OCD-S△OCD
=![]()
=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,用三个正方形①、2个正方形②、1个正方形③和缺了一个角的长方形④,恰好拼成一个大长方形.根据图示数据,解答下列问题:
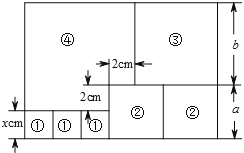
(1)用含x的代数式表示:a=__________cm,b=__________cm;
(2)用含x的代数式表示大长方形的周长,并求x=5时大长方形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某新型节能环保汽车油箱中原有汽油100升,汽车每行驶50千米耗油8升,试写出汽车行驶的路程x(千米)与油箱中剩余油量y(升)之间的函数关系式,并画出这个函数的图象,函数的图象是什么形状?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发市场规定,批发苹果不少于100千克时,批发价为每千克2.5元.小王携带现金3 000元到该市场采购苹果,并以批发价买进.如果购进的苹果是x千克,小王付款后剩余现金y元.
(1)试写出x与y之间的函数关系式,并指出自变量的取值范围;
(2)画出函数图象,指出图象形状和终点坐标;
(3)若小王以每千克3元的价格将苹果卖出,卖出x千克后可获利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上![]() 点表示数
点表示数![]() ,
,![]() 点表示数
点表示数![]() ,
,![]() 满足
满足![]()
![]()
(1)点![]() 表示的数为 ,点
表示的数为 ,点![]() 表示的数为 .
表示的数为 .
(2)若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,请在数轴上找一点
,请在数轴上找一点![]() ,使
,使![]() ,则
,则![]() 表示的数为 .
表示的数为 .
(3)如图,若在原点![]() 处放一挡板,一小球甲从点
处放一挡板,一小球甲从点![]() 处以1个单位/秒的速度向左运动;同时另一小球乙从点
处以1个单位/秒的速度向左运动;同时另一小球乙从点![]() 处以2单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为
处以2单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为![]() (秒),
(秒),
![]()
①分别表示出甲、乙两小球到原点的距离(用![]() 表示);
表示);
②求甲、乙两小球到原点的距离相等时经历的时间.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是最小的正整数,且
是最小的正整数,且![]() 满足
满足![]() ,请回答:
,请回答:
(1)请直接写出![]() 的值:
的值:![]() =______,
=______,![]() =______,
=______,![]() =______;
=______;
(2)在(1)的条件下,若点P为一动点,其对应的数为![]() ,点P在0到2之间运动,即
,点P在0到2之间运动,即![]() 时,化简:
时,化简:![]() ;
;
(3)在(1)(2)的条件下,![]() ,b,c分别对应的点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,假设
,b,c分别对应的点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,假设![]() 秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.请问:BC﹣AB的值是否随着时间
秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.请问:BC﹣AB的值是否随着时间![]() 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌饮水机厂生产一种饮水机和饮水机桶,饮水机每台定价350元,饮水机桶每只定价50元,厂方开展促销活动期间,可以同时向客户提供两种优惠方案:
方案一:买一台饮水机送一只饮水机桶;
方案二:饮水机和饮水机桶都按定价的90%付款.
现某客户到该饮水机厂购买饮水机30台,饮水机桶![]() 只(
只(![]() 超过30).
超过30).
(1)若该客户按方案一购买,求客户需付款(用含![]() 的式子表示);若该客户按方案二购买,求客户需付款(用含
的式子表示);若该客户按方案二购买,求客户需付款(用含![]() 的式子表示);
的式子表示);
(2)若![]() 时,通过计算说明此时按哪种方案购买较为合算?
时,通过计算说明此时按哪种方案购买较为合算?
(3)当![]() 时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,并计算出所需的钱数.
时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,并计算出所需的钱数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某开发区有一块四边形空地ABCD,现计划在空地上种植草皮,经测量,∠B=90°,AB=20m,BC=15m,CD=7m,AD=24m.若每平方米草皮需要200元,则种植这片草皮需要多少元?
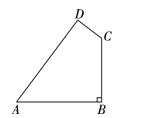
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com