
����Ŀ��ijƷ����ˮ��������һ����ˮ������ˮ��Ͱ����ˮ��ÿ̨����350Ԫ����ˮ��Ͱÿֻ����50Ԫ��������չ������ڼ䣬����ͬʱ��ͻ��ṩ�����Żݷ�����
����һ����һ̨��ˮ����һֻ��ˮ��Ͱ��
����������ˮ������ˮ��Ͱ�������۵�90%����.
��ij�ͻ�������ˮ����������ˮ��30̨����ˮ��Ͱ![]() ֻ��
ֻ��![]() ����30����
����30����
��1�����ÿͻ�������һ������ͻ��踶��ú�![]() ��ʽ�ӱ�ʾ�������ÿͻ���������������ͻ��踶��ú�
��ʽ�ӱ�ʾ�������ÿͻ���������������ͻ��踶��ú�![]() ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����
��2����![]() ʱ��ͨ������˵����ʱ�����ַ��������Ϊ���㣿
ʱ��ͨ������˵����ʱ�����ַ��������Ϊ���㣿
��3����![]() ʱ�����ܸ���һ�ָ�ΪʡǮ�Ĺ�������д����Ĺ�����������������Ǯ����
ʱ�����ܸ���һ�ָ�ΪʡǮ�Ĺ�������д����Ĺ�����������������Ǯ����
���𰸡���1���ͻ�������һ�����踶�50x+9000��Ԫ���ͻ��������������踶�45x+9450��Ԫ����2����x=40ʱ��������һ������㣻��3���Ȱ�����һ����30̨��ˮ������30ֻ��ˮ��Ͱ��10500Ԫ����10ֻ��ˮ��Ͱ��������������450Ԫ������10950Ԫ��
��������
��1�����ն�Ӧ�ķ����ļ��㷽���ֱ��г�����ʽ���ɣ�
��2����x=40������õĴ���ʽ�����ֵ����һ���Ƚϵó��𰸼��ɣ�
��3���������ַ������Żݷ�ʽ���ɵó��Ȱ�����һ����30̨��ˮ������30ֻ��ˮ��Ͱ������10ֻ��ˮ��Ͱ�ٰ����������ɣ�
��1���ͻ�������һ�����踶��30��350+��x��30����50=50x+30��350��50��=��50x+9000��Ԫ��
�ͻ��������������踶��350��90%��30+50��90%��x=��45x+9450��Ԫ��
��2����x=40ʱ������һ��50��40+9000=11000��Ԫ����
��������45��40+9450=11250��Ԫ����
��������һ������㣻
��3���Ȱ�����һ����30̨��ˮ������30ֻ��ˮ��Ͱ��10500Ԫ����10ֻ��ˮ��Ͱ��������������450Ԫ������10950Ԫ��


 ��ѧȫ��������ѵ��ϵ�д�
��ѧȫ��������ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
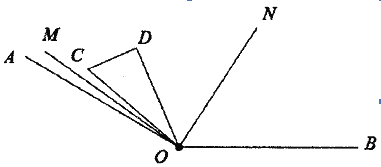
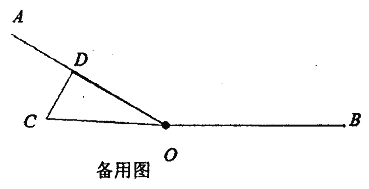
����Ŀ����ͼ����֪![]() ����һ��ֱ��������ֽƬ(
����һ��ֱ��������ֽƬ(![]() )��һ��������ڵ�
)��һ��������ڵ�![]() �����ֽ�������ֽƬ�Ƶ�
�����ֽ�������ֽƬ�Ƶ�![]() ����ת����
����ת����![]() ƽ��б��
ƽ��б��![]() ��
��![]() �ļнǣ�
�ļнǣ�![]() ƽ��
ƽ��![]() .
.
��1����������ֽƬ�Ƶ�![]() ת��(������ֽƬʼ�ձ�����
ת��(������ֽƬʼ�ձ�����![]() ���ڲ�)����
���ڲ�)����![]() ����
����![]() _______��
_______��
��2����������ֽƬ�Ƶ�![]() ת��(������ֽƬʼ�ձ�����
ת��(������ֽƬʼ�ձ�����![]() ���ڲ�)��������
���ڲ�)��������![]() ǡ��ƽ��
ǡ��ƽ��![]() ����
����![]() ����
����![]() �Ķ���;
�Ķ���;
��3����������ֽƬ�Ƶ�![]() ��
��![]() ��
��![]() �غ�λ����ʱ��ת��
�غ�λ����ʱ��ת��![]() ��
��![]() �غϵ�λ�ã�������ת��������
�غϵ�λ�ã�������ת��������![]() ��
��![]() ��������ϵ����˵������.
��������ϵ����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����A��B��C������ͬһֱ���ϣ����߶�AB=6 cm��BC=4 cm����M��N�ֱ�ΪAB��BC���е㣬��ôM��N����֮��ľ���Ϊ( )
A. 5 cm B. 1 cm C. 5��1 cm D. ��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD����O���ڽ��ı��Σ�ACΪֱ����![]() ��DE��BC������ΪE��
��DE��BC������ΪE��

��1����֤��CDƽ����ACE��
��2���ж�ֱ��ED����O��λ�ù�ϵ����˵�����ɣ�
��3����CE=1��AC=4������Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
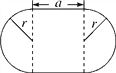
����Ŀ��һ����̳����״��ͼ��ʾ�����������ǰ뾶��ȵİ�Բ����
(1)��̳���ܳ�l��
(2)��̳�����S��
(3)��a��8m��r��5m�����ʱ��̳���ܳ������(��ȡ3.14)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
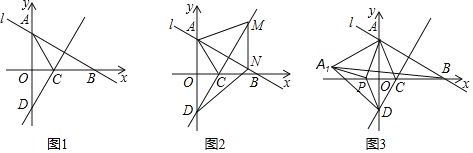
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���ֱ֪��l��y![]() x+3��y���ڵ�A��x���ڵ�B����BAO�Ľ�ƽ����AC��x���ڵ�C������C��ֱ��AB�Ĵ��ߣ���y���ڵ�D��
x+3��y���ڵ�A��x���ڵ�B����BAO�Ľ�ƽ����AC��x���ڵ�C������C��ֱ��AB�Ĵ��ߣ���y���ڵ�D��
��1����ֱ��CD�Ľ���ʽ��
��2����ͼ2������MΪֱ��CD�ϵ�һ�����㣬����M��MN��y�ᣬ��ֱ��AB���N�����ı���AMNDΪ����ʱ������ACM�������
��3����ͼ3����PΪx���ϵ�һ����������PA��PD������ADP��DP���۵õ���A1DP�����Ե�A��A1��BΪ������������ǵ���������ʱ�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��һ���ڱ���ȵ��ı��ν��������Ρ������øö���������¸��⣺
(1) ����
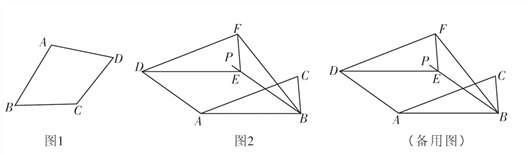
��գ���ͼ1�����ı���ABCD�У�����������������һ������������ı���ABCD�ǡ����Ρ���
��2��Ӧ��
֤�����Խ�������һ���ƽ�ֵġ����Ρ��������Σ����뻭��ͼ�Σ�д����֪����֤��֤����
(3) ��չ
��ͼ2����Rt��ABC�У���ABC��90�㣬AB��2��BC��1����Rt��ABC�ء�ABC��ƽ����BP����ƽ�Ƶõ���DEF������AD��BF����ƽ�ƺ���ı���ABFD�ǡ����Ρ������߶�BE�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ʽ![]() �ij�����ʽ
�ij�����ʽ![]() ,������
,������![]() ,��
,��![]() ����������������Ӧ�ĵ�ΪA��B
����������������Ӧ�ĵ�ΪA��B
(1)�߶�AB�ij�=
(2)��������B���ұ���һ��C����C��A��B����ľ����Ϊ11�����C������������Ӧ������
(3) ��P��Q����ֱ��A��B������ͬʱ�������������˶���P����ٶ���Q���ٶȵ�2������3���2OP=OQ�����Q�˶����ٶ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���С½�� A �س����������г���ͬһ��·��ʻ�� B �أ�����������صľ��� s����ʻʱ��t֮��Ĺ�ϵ��ͼ����ͼ������ͼ��ش��������⣺
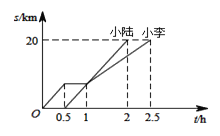
(1) С����;�ж�����ʱ��Ϊ___________h��С½�� A �ص� B �ص��ٶ���________km/h��
(2) ��С���С½����ʱ�������� B �ص�·����____________ǧ�ף�
(3) д��С���ڶ���֮ǰ�� A �ص�·��s����ʻʱ��t֮��ĺ�����ϵʽΪ_____________________.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com