
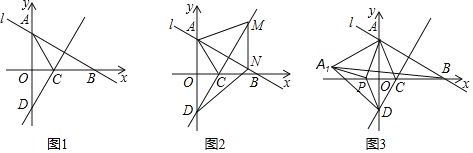
【题目】如图1,在平面直角坐标系中,已知直线l:y![]() x+3交y轴于点A,x轴于点B,∠BAO的角平分线AC交x轴于点C,过点C作直线AB的垂线,交y轴于点D.
x+3交y轴于点A,x轴于点B,∠BAO的角平分线AC交x轴于点C,过点C作直线AB的垂线,交y轴于点D.
(1)求直线CD的解析式;
(2)如图2,若点M为直线CD上的一个动点,过点M作MN∥y轴,交直线AB与点N,当四边形AMND为菱形时,求△ACM的面积;
(3)如图3,点P为x轴上的一个动点连接PA、PD,将△ADP沿DP翻折得到△A1DP,当以点A、A1、B为顶点的三角形是等腰三角形时,求点P的坐标.
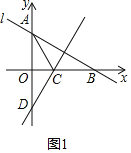
【答案】(1)y![]() x﹣3;(2)
x﹣3;(2)![]() ;(3)点P的坐标为(
;(3)点P的坐标为(![]() ,0),(﹣6﹣3
,0),(﹣6﹣3![]() ),(3
),(3![]() ,0),(6﹣3
,0),(6﹣3![]() ,0).
,0).
【解析】
(1)分别令x、y为0,建立方程可求得A、B的坐标,并由tan∠BAO=![]() ,求得∠BAO=60°,由AC平分∠BAO求得C的坐标,再应用两条直线垂直时,k1k2=-1,就可以求得CD的解析式;
,求得∠BAO=60°,由AC平分∠BAO求得C的坐标,再应用两条直线垂直时,k1k2=-1,就可以求得CD的解析式;
(2)根据菱形对角线互相垂直平分这一性质,可以确定点M的坐标,易求出△ACM的面积;
(3)△AA1B为等腰三角形,分三种情况:①AA1=AB,证明△ADA1是等边三角形解决问题.②A1B=AB.过A1作A1H⊥y轴于H,易证△A1AH≌△APO(AAS),利用全等三角形性质解决问题即可.③AA1=A1B.若点P在x负半轴上,不存在A1B=AB,若点P在x正半轴上,点P与点B重合时,A1B=AB.
(1)如图1,
在y![]() x+3中,令x=0,得y=3,
x+3中,令x=0,得y=3,
∴A(0,3),
令y=0得0![]() x+3,解得x=3
x+3,解得x=3![]() ,
,
∴B(3![]() ,0),
,0),
在Rt△AOB中,∠AOB=90°,
∴∠BAO=60°,
∵AC平分∠BAO,
∴∠CAO![]() ∠BAO=30°
∠BAO=30°
∴OC![]()
∴C(![]() ,0)
,0)
∵CD⊥AB
∴∠ODC=90°﹣∠BAO=90°﹣60°=30°
在Rt△COD中,∠COD=90°,
∴OD=3
∴D(0,﹣3)
设直线CD解析式为y=kx+b,将C(![]() ,0),D(0,﹣3)代入得
,0),D(0,﹣3)代入得
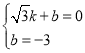 ,解得
,解得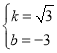
∴直线CD的解析式为y![]() x﹣3.
x﹣3.
(2)如图2,
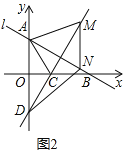
令CD与AB交于点E,∵四边形AMND是菱形,
∴AE=NE DE=ME
解方程组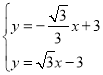 得
得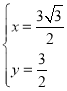 ,
,
∴E(![]() ,
,![]() ),
),
设M(t,![]() t﹣3),则
t﹣3),则![]() ,
,![]() ,∴t=3
,∴t=3![]()
∴M(![]() ,6),
,6),
在Rt△ADE中,cos∠ODC![]() ,sin∠ODC
,sin∠ODC![]()
∴DE=AD×cos∠ODC=6cos30°=3![]() ,AE=ADsin∠ODC=6sin30°=3
,AE=ADsin∠ODC=6sin30°=3
∴![]()
在Rt△ODC中,∠ODC=30°,∴CD=2OC=2![]()
∴CE=DE﹣CD=3![]() 2
2![]()
∴CM=CE+ME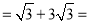 4
4![]() ,
,
∴S△ACM![]() .
.
(3)如图3,
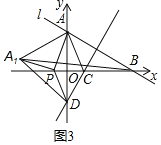
△AA1B为等腰三角形,分三种情况:
①AA1=AB,
由翻折知:A1D=AD=6,A1P=AP,∠ADP=∠A1DP,
∵∠ABO=90°﹣∠BAO=90°﹣60°=30°,
∴AB=2AO=2×3=6
∴AA1=A1D=AD
∴△AA1D是等边三角形
∴∠A1DA=60°,
∴∠ADP=30°,在Rt△PDO中,tan∠ADP![]()
∴OP=OD×tan∠ADP=3tan30°![]()
∴![]()
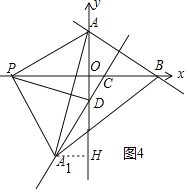
②AA1=A1B
∴A1在线段AB垂直平分线,
易证直线CD垂直平分线段AB
∴点A1落在直线CD上
由翻折知:A1D=AD=6,A1P=AP,∠ADP=∠A1DP,
∵∠ADC=30°,
∴∠ADP=∠A1DP=75°,∠DPO=90°﹣∠ADP=90°﹣75°=15°,
∵OA=OD,PO⊥AD
∴∠APO=∠DPO=15°,
∴∠APD=∠A1PD=30°
∴∠A1PA=60°
∴△A1PA是等边三角形
∴AP=A1A
过A1作A1H⊥y轴于H,易证△A1AH≌△APO(AAS)
A1H=AO=3,AH=OP
点A1B的横坐标为﹣3,将x=﹣3代入直线CD的解析式为y![]() x﹣3中,得y=﹣3
x﹣3中,得y=﹣3![]() 3,
3,
∴OH=3![]() 3,OP=AH=AO+OH=3+3
3,OP=AH=AO+OH=3+3![]() 3=6+3
3=6+3![]() ,
,
∴P(﹣6﹣3![]() ,0)
,0)
③A1B=AB
若点P在x负半轴上,不存在A1B=AB,
若点P在x正半轴上,点P与点B重合时,A1B=AB
∴P(3![]() ,0),
,0),
④如图5中,当AA′=A′B时,易证DP平分∠ODC,可得P(6﹣3![]() ,0)
,0)
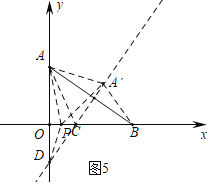
综上所述,点P的坐标为(![]() ,0),(﹣6﹣3
,0),(﹣6﹣3![]() ),(3
),(3![]() ,0),(6﹣3
,0),(6﹣3![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点A,与y轴交于点C.抛物线
与x轴交于点A,与y轴交于点C.抛物线![]() 经过A,C两点,且与x轴交于另一点B(点B在点A右侧).
经过A,C两点,且与x轴交于另一点B(点B在点A右侧).

(1)求抛物线的解析式及点B坐标;
(2)若点M是线段BC上的一动点,过点M的直线EF平行y轴交x轴于点F,交抛物线于点E.求ME长的最大值;
(3)试探究当ME取最大值时,在抛物线上、x轴下方是否存在点P,使以M,F,B,P为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发市场规定,批发苹果不少于100千克时,批发价为每千克2.5元.小王携带现金3 000元到该市场采购苹果,并以批发价买进.如果购进的苹果是x千克,小王付款后剩余现金y元.
(1)试写出x与y之间的函数关系式,并指出自变量的取值范围;
(2)画出函数图象,指出图象形状和终点坐标;
(3)若小王以每千克3元的价格将苹果卖出,卖出x千克后可获利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是最小的正整数,且
是最小的正整数,且![]() 满足
满足![]() ,请回答:
,请回答:
(1)请直接写出![]() 的值:
的值:![]() =______,
=______,![]() =______,
=______,![]() =______;
=______;
(2)在(1)的条件下,若点P为一动点,其对应的数为![]() ,点P在0到2之间运动,即
,点P在0到2之间运动,即![]() 时,化简:
时,化简:![]() ;
;
(3)在(1)(2)的条件下,![]() ,b,c分别对应的点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,假设
,b,c分别对应的点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,假设![]() 秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.请问:BC﹣AB的值是否随着时间
秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.请问:BC﹣AB的值是否随着时间![]() 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌饮水机厂生产一种饮水机和饮水机桶,饮水机每台定价350元,饮水机桶每只定价50元,厂方开展促销活动期间,可以同时向客户提供两种优惠方案:
方案一:买一台饮水机送一只饮水机桶;
方案二:饮水机和饮水机桶都按定价的90%付款.
现某客户到该饮水机厂购买饮水机30台,饮水机桶![]() 只(
只(![]() 超过30).
超过30).
(1)若该客户按方案一购买,求客户需付款(用含![]() 的式子表示);若该客户按方案二购买,求客户需付款(用含
的式子表示);若该客户按方案二购买,求客户需付款(用含![]() 的式子表示);
的式子表示);
(2)若![]() 时,通过计算说明此时按哪种方案购买较为合算?
时,通过计算说明此时按哪种方案购买较为合算?
(3)当![]() 时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,并计算出所需的钱数.
时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,并计算出所需的钱数.
查看答案和解析>>
科目:初中数学 来源: 题型:
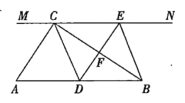
【题目】如图,在![]() 中,
中,![]() ,过点
,过点![]() 的直线
的直线![]() ,
,![]() 为
为![]() 边上一点,过点
边上一点,过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)当![]() 为
为![]() 的中点时,四边形
的中点时,四边形![]() 是什么特殊四边形?请说明你的理由;
是什么特殊四边形?请说明你的理由;
(3)若![]() 为
为![]() 的中点,则当
的中点,则当![]() 的大小满足什么条件时,四边形
的大小满足什么条件时,四边形![]() 是正方形?请说明你的理由.
是正方形?请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某开发区有一块四边形空地ABCD,现计划在空地上种植草皮,经测量,∠B=90°,AB=20m,BC=15m,CD=7m,AD=24m.若每平方米草皮需要200元,则种植这片草皮需要多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四张背面完全相同的纸牌A、B、C、D,其中正面分别画有四个不同的几何图形(如图),小华将这4张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸一张.
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A、B、C、D表示);
(2)求摸出两张纸牌牌面上所画几何图形,既是轴对称图形又是中心对称图形的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为传播“绿色出行,低碳生活”的理念,小贾同学的爸爸从家里出发,骑自行车去图书馆看书,图1表达的是小贾的爸爸行驶的路程![]() (米)与行驶时间
(米)与行驶时间![]() (分钟)的变化关系
(分钟)的变化关系
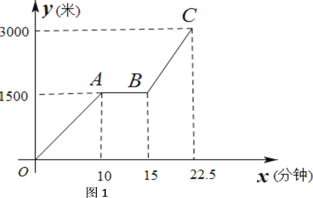
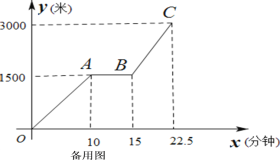
(1)求线段BC所表达的函数关系式;
(2)如果小贾与爸爸同时从家里出发,小贾始终以速度120米/分钟行驶,当小贾与爸爸相距100米是,求小贾的行驶时间;
(3)如果小贾的行驶速度是![]() 米/分,且在途中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出
米/分,且在途中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出![]() 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com