
����Ŀ����֪![]() ����С������������
����������������![]() ����
����![]() ����ش�
����ش�
��1����ֱ��д��![]() ��ֵ��
��ֵ��![]() ��______��
��______��![]() =______��
=______��![]() ��______��
��______��
��2���ڣ�1���������£�����PΪһ���㣬���Ӧ����Ϊ![]() ����P��0��2֮���˶�����
����P��0��2֮���˶�����![]() ʱ������
ʱ������![]() ��
��
��3���ڣ�1����2���������£�![]() ��b��c�ֱ��Ӧ�ĵ�A��B��C��ʼ���������˶�������A��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ����B�͵�C�ֱ���ÿ��2����λ���Ⱥ�5����λ���ȵ��ٶ������˶�������
��b��c�ֱ��Ӧ�ĵ�A��B��C��ʼ���������˶�������A��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ����B�͵�C�ֱ���ÿ��2����λ���Ⱥ�5����λ���ȵ��ٶ������˶�������![]() ���ӹ�������B���C֮��ľ����ʾΪBC����A���B֮��ľ����ʾΪAB�����ʣ�BC��AB��ֵ�Ƿ�����ʱ��
���ӹ�������B���C֮��ľ����ʾΪBC����A���B֮��ľ����ʾΪAB�����ʣ�BC��AB��ֵ�Ƿ�����ʱ��![]() �ı仯���ı䣿���仯����˵�����ɣ������䣬������ֵ��
�ı仯���ı䣿���仯����˵�����ɣ������䣬������ֵ��
![]()
���𰸡���1����1��1��5����2����x+6��3x+8����3�����䣬BC��AB=2.
��������
��1������b����С��������������ȷ��b��ֵ��Ȼ����ݷǸ��������ʣ������Ǹ����ĺ���0����ÿ������0���������a��b��c��ֵ��
��2�����������������x��ȡֵ��Χ��ȷ��x+1��x-1��x-2�ķ��ţ�Ȼ����ݾ���ֵ�����廯�ɣ�
��3���Ȱ�AB��BC�ú�t��ʽʾ�������ٵõ�BC-AB=2���Ӷ��ó�BC-AB��ֵΪ��ֵ��
�⣺��1��������ã�b��1��c��5��0��a+b��0
���a����1�� b��1�� c��5��
�ʴ�Ϊ����1��1��5��
��2������P��0��2֮���˶�ʱ��0��x��2��
��ˣ�������������ۣ�
�ٵ�0��x��1ʱ��x+1��0��x��1��0��x��2��0��
ԭʽ��x+1��1+x+6��3x����x+6��
�ڵ�1��x��2ʱ��x+1��0��x��1��0��x��2��0��
ԭʽ��x+1��x+1+6��3x����3x+8��
���ϣ�����![]() �Ľ��Ϊ��x+6��3x+8��
�Ľ��Ϊ��x+6��3x+8��
��3�����ۣ����䣬BC��AB=2��
���ɣ�
����t�룬��A�����˶���t����λ���ȣ���B�����˶���2t����λ���ȣ���C�����˶���5t����λ���ȣ�����ʼ�˶�֮ǰ��AB=1-(-1)=2��BC=5-1=4,
���˶�t���AB=t+2t+2=3t+2��BC=5t-2t+4=3t+4��
��AB��3t+2��BC��3t+4
��BC��AB����3t+4��-(3t+2)=2
��BC��AB��ֵ���䣬BC��AB=2��


 ͨ��ѧ��Ĭд����ϵ�д�
ͨ��ѧ��Ĭд����ϵ�д� ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
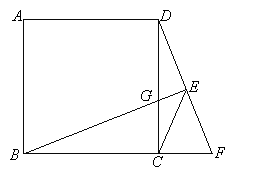
����Ŀ����������ABCD �У���F��BC�ӳ�����һ�㣬����B��BE��DF�ڵ�E����CD�ڵ�G������CE.
��1����������ABCD�߳�Ϊ3��DF=4����CG�ij���
��2����֤��EF+EG=![]() CE.
CE.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���CAB=70�㣬����ABC�Ƶ�A��ʱ����ת����AB��C���λ�ã�ʹ��CC���AB,���BAB��Ķ����ǣ� ��
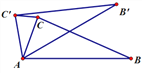
A. 70�� B. 35�� C. 40�� D. 90��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
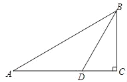
����Ŀ����ͼ������ABC�У���C=90�㣬��A=30�㣬BD�ǡ�ABC��ƽ���ߣ�CD=5cm����AB�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD����O���ڽ��ı��Σ�ACΪֱ����![]() ��DE��BC������ΪE��
��DE��BC������ΪE��

��1����֤��CDƽ����ACE��
��2���ж�ֱ��ED����O��λ�ù�ϵ����˵�����ɣ�
��3����CE=1��AC=4������Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����N(0��6)����M��x�Ḻ�����ϣ�ON��3OM.AΪ�߶�MN��һ�㣬AB��x�ᣬ����Ϊ��B��AC��y�ᣬ����Ϊ��C.
(1)д����M�����ꣻ
(2)��ֱ��MN�ı���ʽ��
(3)����A�ĺ�����Ϊ��1�������ABOC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
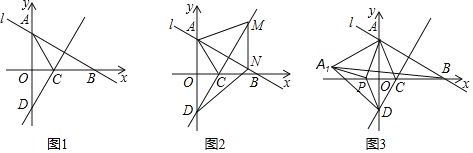
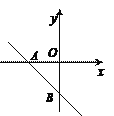
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���ֱ֪��l��y![]() x+3��y���ڵ�A��x���ڵ�B����BAO�Ľ�ƽ����AC��x���ڵ�C������C��ֱ��AB�Ĵ��ߣ���y���ڵ�D��
x+3��y���ڵ�A��x���ڵ�B����BAO�Ľ�ƽ����AC��x���ڵ�C������C��ֱ��AB�Ĵ��ߣ���y���ڵ�D��
��1����ֱ��CD�Ľ���ʽ��
��2����ͼ2������MΪֱ��CD�ϵ�һ�����㣬����M��MN��y�ᣬ��ֱ��AB���N�����ı���AMNDΪ����ʱ������ACM�������
��3����ͼ3����PΪx���ϵ�һ����������PA��PD������ADP��DP���۵õ���A1DP�����Ե�A��A1��BΪ������������ǵ���������ʱ�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��y����x��2��x���ڵ�A����y���ڵ�B��һ�����ߵĶ���ΪA���Ҿ�����B��
��1����������ߵĽ���ʽ��
��2������C��m����4.5�����������ϣ���m��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������мӴ���ְ����Ͷ�����ȣ�ȡ�������õ����Ч����ijУ��������˾��꼶a��ѧ����ѧ�������ݵ�����������ͼ��������������ͳ��ͼ��

�������ͼ����Ϣ����������⣺
��1��a= ;
��2������ͳ��ͼ�У���ְ�ߡ���Ӧ�����ε�Բ�Ľ���= ��
��3���벹ȫ����ͳ��ͼ��
��4������У���꼶��ѧ��900�������Ƹ�У���ж�������ҵ������ѧ������ְ�ߡ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com