
【题目】某水果批发市场规定,批发苹果不少于100千克时,批发价为每千克2.5元.小王携带现金3 000元到该市场采购苹果,并以批发价买进.如果购进的苹果是x千克,小王付款后剩余现金y元.
(1)试写出x与y之间的函数关系式,并指出自变量的取值范围;
(2)画出函数图象,指出图象形状和终点坐标;
(3)若小王以每千克3元的价格将苹果卖出,卖出x千克后可获利润多少元?
【答案】(1)![]() ;(2)见解析;(3)0.5x元.
;(2)见解析;(3)0.5x元.
【解析】
(1`)利用已知批发价为每千克2.5元,小王携带现金3000元到这个市场采购苹果,求出解析式,根据剩余现金=总现金数-购买苹果费用,根据购买千克数应不少于100以及剩余现金为非负数可得自变量的取值;
(2)根据(1)中一次函数解析式,利用“两点确定一条直线”作出图象,注意x的取值范围;
(3)先求出售出每千克苹果的利润,再求出总利润即可.
(1) 由已知批发价为每千克2.5元,小王携带现金3000元到这个市场采购苹果得y与x的函数关系式:y=3000-2.5x,
∵批发苹果不少于100千克时,批发价为每千克2.5元,
∴x≥100kg,
∴至多可以买3000÷2.5=1200kg.
故自变量x的取值范围:100≤x≤1200..
(2) 令x=0,则y=3000;令y=0,则x=1200,
所以该直线经过点(0,3000),(1200,0),其图象如图所示:

图象是一条线段,终点坐标为(1200,0).
(3)根据题意得,小王购进的苹果单价是每千克2.5元,售价是每千克3元,
因此,每千克苹果的利润为:3-2.5=0.5元,
现在小王卖出苹果x千克,
因此获利0.5x元.


科目:初中数学 来源: 题型:
【题目】已知,如图,在坡顶A处的同一水平面上有一座古塔BC,数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°,然后他们沿着坡度为1:2.4的斜坡AP攀行了26米,在坡顶A处又测得该塔的塔顶B的仰角为76°.
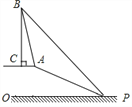
求:(1)坡顶A到地面PO的距离;
(2)古塔BC的高度(结果精确到1米).
(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级三班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6个型号)
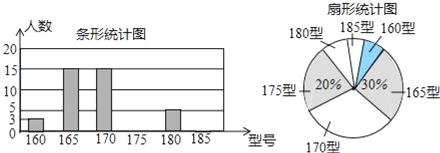
根据以上信息,解答下列问题:
(1)该班共有 名学生;
(2)在扇形统计图中,185型校服所对应的扇形圆心角的大小为 ;
(3)该班学生所穿校服型号的众数为 ,中位数为 ;
(4)如果该校预计招收新生600名,根据样本数据,估计新生穿170型校服的学生大约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数是( )
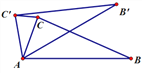
A. 70° B. 35° C. 40° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果A、B、C三点在同一直线上,且线段AB=6 cm,BC=4 cm,若M,N分别为AB,BC的中点,那么M,N两点之间的距离为( )
A. 5 cm B. 1 cm C. 5或1 cm D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是⊙O的内接四边形,AC为直径,![]() ,DE⊥BC,垂足为E.
,DE⊥BC,垂足为E.

(1)求证:CD平分∠ACE;
(2)判断直线ED与⊙O的位置关系,并说明理由;
(3)若CE=1,AC=4,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,已知直线l:y![]() x+3交y轴于点A,x轴于点B,∠BAO的角平分线AC交x轴于点C,过点C作直线AB的垂线,交y轴于点D.
x+3交y轴于点A,x轴于点B,∠BAO的角平分线AC交x轴于点C,过点C作直线AB的垂线,交y轴于点D.
(1)求直线CD的解析式;
(2)如图2,若点M为直线CD上的一个动点,过点M作MN∥y轴,交直线AB与点N,当四边形AMND为菱形时,求△ACM的面积;
(3)如图3,点P为x轴上的一个动点连接PA、PD,将△ADP沿DP翻折得到△A1DP,当以点A、A1、B为顶点的三角形是等腰三角形时,求点P的坐标.
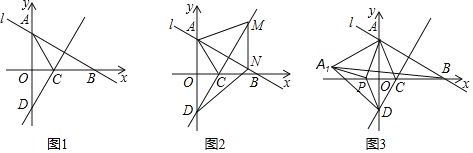
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习完一次函数后,小荣遇到过这样的一个新颖的函数:y=|x-1|,小荣根据学校函数的经验,对函数y=|x-1|的图象与性质进行了探究。下面是小荣的探究过程,请补充完成
列表:下表是y与的几组对应值,请补充完整。

(2)描点连线:在平面直角坐标系xOy中,请描出以上表中各对对应值为坐标的点,画出该函数的图象;
(3)进一步探究发现,该函数图象的最低点的坐标是(1,0),结合图数的图象,写出该函数的其他性质(一条即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com