
【题目】小李和小陆从 A 地出发,骑自行车沿同一条路行驶到 B 地,他们离出发地的距离 s和行驶时间t之间的关系的图象如图,根据图象回答下列问题:
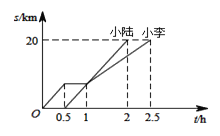
(1) 小李在途中逗留的时间为___________h,小陆从 A 地到 B 地的速度是________km/h;
(2) 当小李和小陆相遇时,他们离 B 地的路程是____________千米;
(3) 写出小李在逗留之前离 A 地的路程s和行驶时间t之间的函数关系式为_____________________.
【答案】(1)0.5,![]() ; (2)
; (2)![]() ;(3)
;(3)![]()
【解析】
试题(1)通过观察图象可得到距离没有发生变化的即为逗留的时间;用路程除以时间即可得出小陆的速度;
(2)根据速度一定,路程与时间成正比即可求解;
(3)如图,求出N点坐标,即可得出M点坐标,从而可求出小李在逗留之前离 A 地的路程s和行驶时间t之间的函数关系式.
试题解析:()1如图所示,

线段MN说明小李在行驶过程中停留的时间为(1-0.5)=0.5小时.
小陆从 A 地到 B 地的速度是20÷(2-0.5)=![]() km/小时.
km/小时.
(2)20-![]() ×(1-0.5)=
×(1-0.5)=![]() km;
km;
(3)易知N(1, ![]() ),所以M(0.5,
),所以M(0.5,![]() )
)
设OM的函数关系式为s=kt
把M(0.5,![]() )代入s=kt得:k=
)代入s=kt得:k=![]() .
.
∴小李在逗留之前离 A 地的路程s和行驶时间t之间的函数关系式为![]()


科目:初中数学 来源: 题型:
【题目】某品牌饮水机厂生产一种饮水机和饮水机桶,饮水机每台定价350元,饮水机桶每只定价50元,厂方开展促销活动期间,可以同时向客户提供两种优惠方案:
方案一:买一台饮水机送一只饮水机桶;
方案二:饮水机和饮水机桶都按定价的90%付款.
现某客户到该饮水机厂购买饮水机30台,饮水机桶![]() 只(
只(![]() 超过30).
超过30).
(1)若该客户按方案一购买,求客户需付款(用含![]() 的式子表示);若该客户按方案二购买,求客户需付款(用含
的式子表示);若该客户按方案二购买,求客户需付款(用含![]() 的式子表示);
的式子表示);
(2)若![]() 时,通过计算说明此时按哪种方案购买较为合算?
时,通过计算说明此时按哪种方案购买较为合算?
(3)当![]() 时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,并计算出所需的钱数.
时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,并计算出所需的钱数.
查看答案和解析>>
科目:初中数学 来源: 题型:
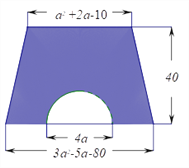
【题目】如图,梯形的上底为![]() +2
+2![]() -10,下底为3
-10,下底为3![]() -5
-5![]() -80,高为40.(
-80,高为40.(![]() 取3)
取3)
(1)用式子表示图中阴影部分的面积;
(2)当![]() =10时,求阴影部分面积的值。
=10时,求阴影部分面积的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列有理数:![]() ,-4,2.5,-1,0,3,
,-4,2.5,-1,0,3,![]() ,5
,5
(1)画数轴,并在数轴上表示这些数:
(2)这些数中最小的数是________,指出这些数中互为相反数的两个数之间所有的整数共有________个
(3)计算出![]() ,-4,2.5,-1,0,3,
,-4,2.5,-1,0,3,![]() ,5这些数的和的绝对值.
,5这些数的和的绝对值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为传播“绿色出行,低碳生活”的理念,小贾同学的爸爸从家里出发,骑自行车去图书馆看书,图1表达的是小贾的爸爸行驶的路程![]() (米)与行驶时间
(米)与行驶时间![]() (分钟)的变化关系
(分钟)的变化关系
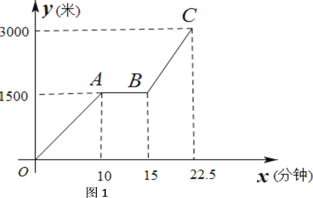
(1)求线段BC所表达的函数关系式;
(2)如果小贾与爸爸同时从家里出发,小贾始终以速度120米/分钟行驶,当小贾与爸爸相距100米是,求小贾的行驶时间;
(3)如果小贾的行驶速度是![]() 米/分,且在途中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出
米/分,且在途中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学有一块四边形的空地ABCD,如图所示,经测量∠A=90°,AB=6m,BC=24m,CD=26m,DA=8m.
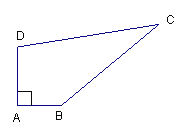
(1)求四边形ABCD的面积;
(2)学校计划在空地上种植草皮,若每平方米草皮需要200元,问学校需要投入多少资金买草皮
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前“微信”、“支付宝”、“共享单车”和“网购”给我们带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行了调查,随机调查了![]() 人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.

(1)根据图中信息求出![]() =___________,
=___________,![]() =_____________;
=_____________;
(2)请你帮助他们将这两个统计图补全;
(3)根据抽样调查的结果,请估算全校2000名学生种,大约有多少人最认可“微信”这一新生事物?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com