
【题目】如图(1),平面直角坐标系中,点A、B分别在x、y轴上,点B的坐标为(0,1),∠BAO=30°.

(1)求AB的长度;
(2)以AB为一边作等边△ABE,作OA的垂直平分线MN交AB的垂线AD于点,求证:BD=OE;
(3)在(2)的条件下,连接DE交AB于F,求证:F为DE的中点.
【答案】(1)2;(2)见解析;(3)见解析.
【解析】
(1)直接运用直角三角形30°角的性质即可.
(2)连接OD,易证△ADO为等边三角形,再证△ABD≌△AEO即可.
(3)作EH⊥AB于H,先证△ABO≌△AEH,得AO=EH,再证△AFD≌△EFH即可.
(1)解:∵在Rt△ABO中,∠BAO=30°,
∴AB=2BO=2;
(2)证明:连接OD,

∵△ABE为等边三角形,
∴AB=AE,∠EAB=60°,
∵∠BAO=30°,作OA的垂直平分线MN交AB的垂线AD于点D,
∴∠DAO=60°.
∴∠EAO=∠NAB
又∵DO=DA,
∴△ADO为等边三角形.
∴DA=AO.
在△ABD与△AEO中,
∵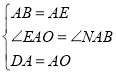 ,
,
∴△ABD≌△AEO(SAS).
∴BD=OE.
(3)证明:作EH⊥AB于H.
∵AE=BE,∴AH=![]() AB,
AB,
∵BO=![]() AB,∴AH=BO,
AB,∴AH=BO,
在Rt△AEH与Rt△BAO中,
![]() ,
,
∴Rt△AEH≌Rt△BAO(HL),
∴EH=AO=AD.
又∵∠EHF=∠DAF=90°,
在△HFE与△AFD中,
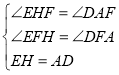 ,
,
∴△HFE≌△AFD(AAS),
∴EF=DF.
∴F为DE的中点.
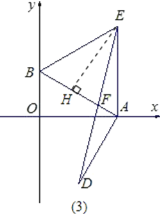


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1关于点B的中心对称得C2,C2与x轴交于另一点C,将C2关于点C的中心对称得C3,连接C1与C3的顶点,则图中阴影部分的面积为_____.

【答案】32
【解析】试题分析:∵抛物线y=﹣x2﹣2x+3与x轴交于点A、B,
∴当y=0时,则﹣x2﹣2x+3=0,
解得x=﹣3或x=1,
则A,B的坐标分别为(﹣3,0),(1,0),
AB的长度为4,
从C1,C3两个部分顶点分别向下作垂线交x轴于E、F两点.
根据中心对称的性质,x轴下方部分可以沿对称轴平均分成两部分补到C1与C2.
如图所示,阴影部分转化为矩形.
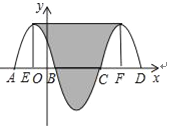
根据对称性,可得BE=CF=4÷2=2,则EF=8
利用配方法可得y=﹣x2﹣2x﹣3=﹣(x+1)2+4
则顶点坐标为(﹣1,4),即阴影部分的高为4,
S阴=8×4=32.
考点:抛物线与x轴的交点.
【题型】填空题
【结束】
17
【题目】解方程:(1)2(3x﹣1)=16;(2)![]() ;(3)
;(3)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前“微信”、“支付宝”、“共享单车”和“网购”给我们带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行了调查,随机调查了![]() 人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.

(1)根据图中信息求出![]() =___________,
=___________,![]() =_____________;
=_____________;
(2)请你帮助他们将这两个统计图补全;
(3)根据抽样调查的结果,请估算全校2000名学生种,大约有多少人最认可“微信”这一新生事物?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图a是一个三角形,分别连接这个三角形三边的中点得到图b;再分别连接图b中间小三角形的三边的中点,得到图c
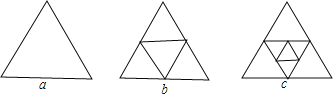
(1)图b有 个三角形,图c有 个三角形.
(2)按上面的方法继续下去,第n个图形中有多少个三角形(用n的代数式表示结论).
(3)当n=10时,第10个图形中有多少个三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆出租车从A地出发,在一条东西走向的街道上往返,每次行驶的路程(记向东为正)记录如下(x>6且x<14,单位:km):

(1)写出这辆出租车每次行驶的方向;
(2)求经过连续4次行驶后,这辆出租车所在的位置(结果可用x表示);
(3)这辆出租车一共行驶了多少路程(结果用x表示)?
查看答案和解析>>
科目:初中数学 来源: 题型:
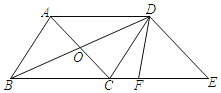
【题目】如图,在平行四边形ABCD中,对角线AC,BD交于点O,OA,OD满足等式![]() +(OA-5)2=0,AD=13.
+(OA-5)2=0,AD=13.
(1)求证:平行四边形ABCD是菱形;
(2)过点D作DE∥AC交BC的延长线于点E,DF平分∠BDE,请求出DF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小强洗漱时的侧面示意图,洗漱台(矩形ABCD)靠墙摆放,高AD=80cm,宽AB=48cm,小强身高166cm,下半身FG=100cm,洗漱时下半身与地面成80°(∠FGK=80°),身体前倾成125°(∠EFG=125°),脚与洗漱台距离GC=15cm(点D,C,G,K在同一直线上).
(1)此时小强头部E点与地面DK相距多少?
(2)小强希望他的头部E恰好在洗漱盆AB的中点O的正上方,他应向前或后退多少?
(sin80°≈0.98,cos80°≈0.17, ![]() ≈1.41,结果精确到0.1cm)
≈1.41,结果精确到0.1cm)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图已知数轴上点![]() 、
、![]() 分别表示
分别表示![]() 、
、![]() ,且
,且![]() 与
与![]() 互为相反数,
互为相反数,![]() 为原点.
为原点.
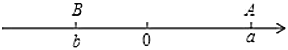
(1)![]() ______,
______,![]() ______;
______;
(2)将数轴沿某个点折叠,使得点![]() 与表示-10的点重合,则此时与点
与表示-10的点重合,则此时与点![]() 重合的点所表示的数为______;
重合的点所表示的数为______;
(3)若点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,点
同时出发,点![]() 以每秒1个单位长度的速度沿数轴向左匀速运动,点
以每秒1个单位长度的速度沿数轴向左匀速运动,点![]() 以每秒2个单位长度的速度沿数轴向右匀速运动,
以每秒2个单位长度的速度沿数轴向右匀速运动,![]() 到点
到点![]() 后立刻原速返回,设运动时间为
后立刻原速返回,设运动时间为![]() 秒.
秒.
①点![]() 表示的数是______(用含
表示的数是______(用含![]() 的代数式表示);
的代数式表示);
②求![]() 为何值时,
为何值时,![]() ;
;
③求![]() 为何值时,点
为何值时,点![]() 与
与![]() 相距3个单位长度.
相距3个单位长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com