
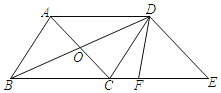
【题目】如图,在平行四边形ABCD中,对角线AC,BD交于点O,OA,OD满足等式![]() +(OA-5)2=0,AD=13.
+(OA-5)2=0,AD=13.
(1)求证:平行四边形ABCD是菱形;
(2)过点D作DE∥AC交BC的延长线于点E,DF平分∠BDE,请求出DF的长度.
【答案】(1)见解析;(2)DF=![]() .
.
【解析】
(1)根据非负性得出OA=5,OD=12,利用勾股定理的逆定理得出AC⊥BD,利用菱形的判定解答;
(2)作辅助线,构建等腰直角三角形,则△FDG为等腰直角三角形,设FG=x,则BG=24-x,证明△BOC∽△BGF,可得x的值,从而得DF的长.
(1)∵![]() +(OA-5)2=0,
+(OA-5)2=0,
∴OA=5,OD=12,
∴OA2+OD2=52+122=169,
∵AD=13,
∴AD2=169,
∴OA2+OD2=AD2,
∴∠AOD=90°,
∴AC⊥BD,
∴平行四边形ABCD是菱形;
(2)过F作FG⊥BD于G,
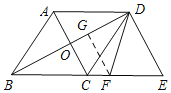
∵DE∥AC,AC⊥BD,
∴BD⊥DE,即∠BDE=90°,
∵DF平分∠BDE,
∴∠BDF=45°,
∴△FDG为等腰直角三角形,
∴DG=FG,
设FG=x,则BG=24-x,
∵OC∥FG,
∴△BOC∽△BGF,
∴![]() ,
,
∴![]() ,x=
,x=![]() ,
,
∴DF=![]() FG=
FG=![]() x=
x=![]() .
.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案科目:初中数学 来源: 题型:
【题目】已知一次函数y=(2m+1)x+m﹣3
(1)若函数图象经过原点,求m的值;
(2)若函数图象与y轴的交点坐标为(0,﹣2),求m的值;
(3)若y随着x的增大而增大,求m的取值范图;
(4)若函数图象经过第一、三,四象限,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,是两种长方形铝合金窗框,已知窗框的长都是y米,窗框的宽都是x米,若一用户需(1)型的窗框2个,(2)型的窗框2个.
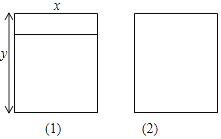
(1)用含x、y的式子表示共需铝合金的长度;
(2)若1m铝合金的平均费用为100元,求当x=1.2,y=1.5时,铝合金的总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
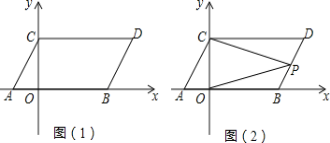
【题目】如图(1),平面直角坐标系中,点A、B分别在x、y轴上,点B的坐标为(0,1),∠BAO=30°.

(1)求AB的长度;
(2)以AB为一边作等边△ABE,作OA的垂直平分线MN交AB的垂线AD于点,求证:BD=OE;
(3)在(2)的条件下,连接DE交AB于F,求证:F为DE的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,在平面直角坐标系中,点
,在平面直角坐标系中,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,将线段
,将线段![]() 先向上平移
先向上平移![]() 个单位长度,再向右平移
个单位长度,再向右平移![]() 个单位长度,得到线段
个单位长度,得到线段![]() ,连接
,连接![]() ,
,![]() ,构成平行四边形
,构成平行四边形![]() .
.
(1)请写出点![]() 的坐标为________,点
的坐标为________,点![]() 的坐标为________,
的坐标为________,![]() ________;
________;
(2)点![]() 在
在![]() 轴上,且
轴上,且![]() ,求出点
,求出点![]() 的坐标;
的坐标;
(3)如图![]() ,点
,点![]() 是线段
是线段![]() 上任意一个点(不与
上任意一个点(不与![]() 、
、![]() 重合),连接
重合),连接![]() 、
、![]() ,试探索
,试探索![]() 、
、![]() 、
、![]() 之间的关系,并证明你的结论.
之间的关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知直线![]() 与x轴、y轴分别交于A、B两点,点C是y轴上一点
与x轴、y轴分别交于A、B两点,点C是y轴上一点![]() 将坐标平面沿直线AC折叠,使点B刚好落在x负半轴上,则点C的坐标为
将坐标平面沿直线AC折叠,使点B刚好落在x负半轴上,则点C的坐标为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
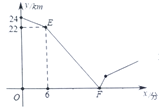
【题目】甲、乙两人在笔直的道路![]() 上相向而行,甲骑自行车从
上相向而行,甲骑自行车从![]() 地到
地到![]() 地,乙驾车从
地,乙驾车从![]() 地到
地到![]() 地,假设他们分别以不同的速度匀速行驶,甲先出6分钟后,乙才出发,乙的速度为
地,假设他们分别以不同的速度匀速行驶,甲先出6分钟后,乙才出发,乙的速度为![]() 千米/分,在整个过程中,甲、乙两人之间的距离
千米/分,在整个过程中,甲、乙两人之间的距离![]() (千米)与甲出发的时间
(千米)与甲出发的时间![]() (分)之间的部分函数图象如图.
(分)之间的部分函数图象如图.
(1)![]() 两地相距______千米,甲的速度为______千米/分;
两地相距______千米,甲的速度为______千米/分;
(2)直接写出点![]() 的坐标______,求线段
的坐标______,求线段![]() 所表示的
所表示的![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(3)当乙到达终点![]() 时,甲还需______分钟到达终点
时,甲还需______分钟到达终点![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点E、F在BD上,且BF=DE.
(1)写出图中所有你认为全等的三角形;
(2)延长AE交BC的延长线于G,延长CF交DA的延长线于H(请补全图形),证明四边形AGCH是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,反比例函数y=![]() (x>0),过点A(3,4).
(x>0),过点A(3,4).
(1)求y关于x的函数表达式.
(2)求当y≥2时,自变量x的取值范围.
(3)在x轴上有一点P(1,0),在反比例函数图象上有一个动点Q,以PQ为一边作一个正方形PQRS,当正方形PQRS有两个顶点在坐标轴上时,画出状态图并求出相应S点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com