
【题目】已知一次函数y=(2m+1)x+m﹣3
(1)若函数图象经过原点,求m的值;
(2)若函数图象与y轴的交点坐标为(0,﹣2),求m的值;
(3)若y随着x的增大而增大,求m的取值范图;
(4)若函数图象经过第一、三,四象限,求m的取值范围.
【答案】(1)m=3;(2)m=1;(3)m>﹣0.5;(4)﹣0.5<m<3.
【解析】
(1)经过原点,则m-3=0,求得其值即可;
(2)若函数图象与y轴的交点坐标为(0,﹣2),即为m-3=-2;
(3)y随着x的增大而增大,就是![]() ,从而求得解集;
,从而求得解集;
(4)函数图象经过第一、三,四象限,k>0,b≤0,求得m的取值范围即可.
解:(1)把(0,0)代入y=(2m+1)x+m﹣3得m﹣3=0,
解得m=3;
(2)把x=0代入y=(2m+1)x+m﹣3得y=m﹣3,则直线y=(2m+1)x+m﹣3与y轴的交点坐标为(0,m﹣3),
所以m﹣3=﹣2,
解得m=1;
(3)∵y随着x的增大而增大,
∴2m+1>0,
解得:m>﹣0.5;
(4)由题意可得: ![]()
解得:![]()
即当![]() 时函数图象经过第一、三,四象限.
时函数图象经过第一、三,四象限.


科目:初中数学 来源: 题型:
【题目】课本例题
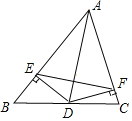
已知:如图,AD是![]() 的角平分线,
的角平分线,![]() ,
,![]() ,垂足分别为E、F.求证:AD垂直平分EF.
,垂足分别为E、F.求证:AD垂直平分EF.
小明做法
证明:因为AD是![]() 的角平分线,
的角平分线,![]() ,
,![]() ,所以
,所以![]()
理由是:“角平分线上的点到这个角的两边的距离相等”.
因为![]() ,
,
所以AD垂直平分EF.
理由是:“到线段两个端点距离相等的点在这条线段的垂直平分线上”.
老师观点
老师说:小明的做法是错误的![]()
请你解决
![]() 指出小明做法的错误;
指出小明做法的错误;
![]() 正确、完整的解决这道题.
正确、完整的解决这道题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为线段
为线段![]() 上一动点,分别过点
上一动点,分别过点![]() 作
作![]() ,
,![]() ,连接
,连接![]() .已知
.已知![]() ,设
,设![]() .
.
(1)用含![]() 的代数式表示
的代数式表示![]() 的值;
的值;
(2)探究:当点![]() 满足什么条件时,
满足什么条件时,![]() 的值最小?最小值是多少?
的值最小?最小值是多少?
(3)根据(2)中的结论,请构造图形求代数式![]() 的最小值.
的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
(1)从图中任找两组全等三角形;
(2)从(1)中任选一组进行证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器公司计划装运甲、乙、丙三种家电到农村销售(规定每辆汽车按规定满载,且每辆汽车只能装同一种家电).下表所示为装运甲、乙、丙三种家电的台数及利润.
甲 | 乙 | 丙 | |
每辆汽车能装运的台数 | 40 | 20 | 30 |
每台家电可获利润(万元) | 0.05 | 0.07 | 0.04 |
(1)若用8辆汽车装运乙、丙两种家电190台到A地销售,问装运乙、丙的汽车各多少辆.
(2)计划用20辆汽车装运甲、乙、丙三种家电720台到B地销售,如何安排装运,可使公司获得36.6万元的利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黔东南州某中学为了解本校学生平均每天的课外学习实践情况,随机抽取部分学生进行问卷调查,并将调查结果分为A,B,C,D四个等级,设学生时间为t(小时),A:t<1,B:1≤t<1.5,C:1.5≤t<2,D:t≥2,根据调查结果绘制了如图所示的两幅不完整的统计图.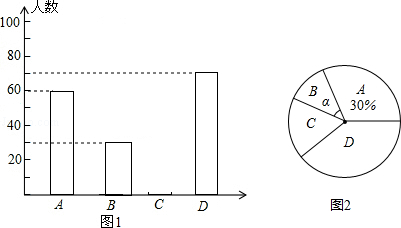
请你根据图中信息解答下列问题:
(1)本次抽样调查共抽取了多少名学生?并将条形统计图补充完整;
(2)本次抽样调查中,学习时间的中位数落在哪个等级内?
(3)表示B等级的扇形圆心角α的度数是多少?
(4)在此次问卷调查中,甲班有2人平均每天课外学习时间超过2小时,乙班有3人平均每天课外学习时间超过2小时,若从这5人中任选2人去参加座谈,试用列表或化树状图的方法求选出的2人来自不同班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料并解答下列问题.
你知道吗?一些代数恒等式可以用平面图形的面积来表示,例如(2a+b)(a+b)=2a2+3ab+b2就可以用图甲中的①或②的面积表示.
(1)请写出图乙所表示的代数恒等式;
(2)画出一个几何图形,使它的面积能表示(a+b)(a+3b)=a2+4ab+3b2;
(3)请仿照上述式子另写一个含有a,b的代数恒等式,并画出与之对应的几何图形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com