
【题目】黔东南州某中学为了解本校学生平均每天的课外学习实践情况,随机抽取部分学生进行问卷调查,并将调查结果分为A,B,C,D四个等级,设学生时间为t(小时),A:t<1,B:1≤t<1.5,C:1.5≤t<2,D:t≥2,根据调查结果绘制了如图所示的两幅不完整的统计图.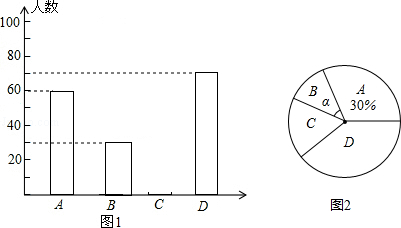
请你根据图中信息解答下列问题:
(1)本次抽样调查共抽取了多少名学生?并将条形统计图补充完整;
(2)本次抽样调查中,学习时间的中位数落在哪个等级内?
(3)表示B等级的扇形圆心角α的度数是多少?
(4)在此次问卷调查中,甲班有2人平均每天课外学习时间超过2小时,乙班有3人平均每天课外学习时间超过2小时,若从这5人中任选2人去参加座谈,试用列表或化树状图的方法求选出的2人来自不同班级的概率.
【答案】
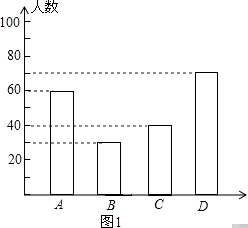
(1)
解:共调查的中学生数是:60÷30%=200(人)
如图所示:
(2)
解:本次抽样调查中,学习时间的中位数落在C等级内
(3)
解:根据题意得:α= ![]() ×360°=54°
×360°=54°
(4)
解:设甲班学生为A1,A2,乙班学生为B1,B2,B3,
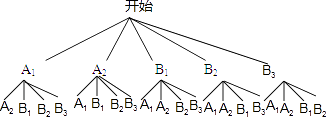
一共有20种等可能结果,其中2人来自不同班级共有12种,
∴P(2人来自不同班级)= ![]() =
= ![]()
【解析】(1)根据B类的人数和所占的百分比即可求出总数;求出C的人数从而补全统计图;(2)根据中位数定义:将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数可得答案;(3)用B的人数除以总人数再乘以360°,即可得到圆心角α的度数;(4)先设甲班学生为A1 , A2 , 乙班学生为B1 , B2 , B3根据题意画出树形图,再根据概率公式列式计算即可.


科目:初中数学 来源: 题型:
【题目】某超市计划经销一些特产,经销前,围绕“A:王高虎头鸡,B:羊口咸蟹子,C:桂河芹菜,D:巨淀湖咸鸭蛋”四种特产,在全市范围内随机抽取了部分市民进行问卷调查:“我最喜欢的特产是什么?”(必选且只选一种).现将调查结果整理后,绘制成如图所示的不完整的扇形统计图和条形统计图. 
(1)请补全扇形统计图和条形统计图;
(2)若全市有110万市民,估计全市最喜欢“羊口咸蟹子”的市民约有多少万人?
(3)在一个不透明的口袋中有四个分别写上四种特产标记A、B、C、D的小球(除标记外完全相同),随机摸出一个小球然后放回,混合摇匀后,再随机摸出一个小球,则两次都摸到A的概率是多少?写出分析计算过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在,苏宁商场进行促销活动,出售一种优惠购物卡(注:此卡只作为购物优惠凭证不能顶替货款),花300元买这种卡后,凭卡可在这家商场按标价的8折购物.
(1)顾客购买多少元金额的商品时,买卡与不买卡花钱相等?在什么情况下购物合算?
(2)小张要买一台标价为3500元的冰箱,如何购买合算?小张能节省多少元钱?
(3)小张按合算的方案,把这台冰箱买下,如果商场还能盈利25%,这台冰箱的进价是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=(2m+1)x+m﹣3
(1)若函数图象经过原点,求m的值;
(2)若函数图象与y轴的交点坐标为(0,﹣2),求m的值;
(3)若y随着x的增大而增大,求m的取值范图;
(4)若函数图象经过第一、三,四象限,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市第一次用4600元购进甲、乙两种商品,其中甲商品件数的2倍比乙商品件数的3倍少40件,甲、乙两种商品的进价和售价如下表(利润=售价﹣进价):
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 28 | 40 |
(1)该超市第一次购进甲、乙两种商品的件数分别是多少?
(2)该超市将第一次购进的甲、乙两种商品全部卖出后一共可获得多少利润?
(3)该超市第二次以同样的进价又购进甲、乙两种商品.其中甲商品件数是第一次的2倍,乙商品的件数不变.甲商品按原价销售,乙商品打折销售.第二次甲、乙两种商品销售完以后获得的利润比第一次获得的利润多280元,则第二次乙商品是按原价打几折销售的?
查看答案和解析>>
科目:初中数学 来源: 题型:
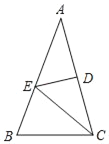
【题目】如图,在△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC,若CE=5,则BC等于( )
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图①,在直角三角形ABC中,∠BAC=90°,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明);
特例探究:如图②,∠MAN=90°,射线AE在这个角的内部,点B、C在∠MAN的边AM、AN上,且AB=AC, CF⊥AE于点F,BD⊥AE于点D.证明:△ABD≌△CAF;
归纳证明:如图③,点BC在∠MAN的边AM、AN上,点EF在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC, ∠1=∠2=∠BAC.求证:△ABE≌△CAF;
拓展应用:如图④,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,则△ACF与△BDE的面积之和为 .(12分)




查看答案和解析>>
科目:初中数学 来源: 题型:
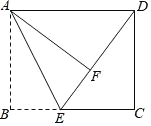
【题目】如图,在长方形 ABCD 中,AB=8,AD=10,点 E 为 BC 上一点,将△ABE 沿 AE 折叠,使点 B 落在长方形内点 F 处, 且 DF=6,求 BE 的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com