
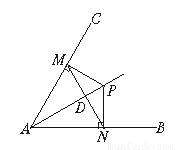
如图所示,P为∠BAC平分线上一点,PM⊥AC于M点,PN⊥AB于N点,MN交AP于D点,要证明MD=ND,只要证_________≌_________,或_________≌_________.而要证明其中一对三角形全等,又必须先证明_________≌_________.由已知条件,只要用“_________”的判定定理就可以证其全等,由此看来,图中共有_________对全等三角形,进一步深思:直线AP与直线MN还可以证明互相_________.
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:
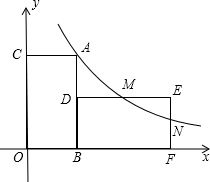 线y=
线y=| k |
| x |
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:河北省模拟题 题型:解答题
 的图象上,且AC =2。
的图象上,且AC =2。 的解析式;
的解析式;
查看答案和解析>>
科目:初中数学 来源:2011年河北省唐山市丰南区中考数学一模试卷(解析版) 题型:解答题
 的图象上,且AC=2.
的图象上,且AC=2. 的解析式.
的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com