
【题目】如图1,![]() ,点
,点![]() 为
为![]() 、
、![]() 之间一点,连接
之间一点,连接![]() 、
、![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,
,![]() 、
、![]() 交于点
交于点![]() ,
,![]()
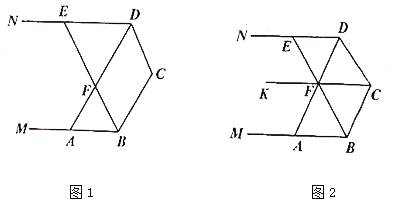
(1)求证:![]() ;
;
(2)如图2连接![]() 并延长至点
并延长至点![]() 若
若![]() ,请直接写出图中所有与
,请直接写出图中所有与![]() 相等的角.
相等的角.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)由角平分线定义得![]() ,
,![]() ,由平行线的性质得
,由平行线的性质得![]() ,然后可证
,然后可证![]() ,从而
,从而![]() ;
;
(2)先证明ND∥KC,然后根据平行线的性质分析证明即可.
解:(1)∵![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)![]() .
.
∵![]() ,∠CDF=∠NDF,
,∠CDF=∠NDF,
∴∠KFA=∠NDF,
∴ND∥KC.
∵![]() ,
,
∴∠BCF=∠DFC=∠NDA,
∠ABC=180°-∠BAD=180°-∠AFK=180°-∠CDF.
∵∠BCD=∠BCF+∠DCF =∠NDA+∠DCF=180°-∠CDF,
∴∠ABC=∠BCD;
∵![]() ,
,
∴∠ABC=∠MAD,
∵ND∥KC,ND∥MB,
∴KC∥MB,
∴∠AFC=∠MAF, ∠KFD=∠MAF,
∴∠ABC=∠BCD=∠AFC=∠MAF=∠KFD.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
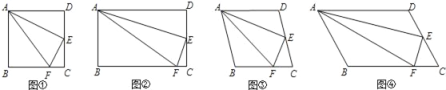
【题目】小明在研究正方形的有关问题时发现有这样一道题:“如图①,在正方形ABCD中,点E是CD的中点,点F是BC边上的一点,且∠FAE=∠EAD.你能够得出什么样的正确的结论?”
(1)小明经过研究发现:EF⊥AE.请你对小明所发现的结论加以证明;
(2)小明之后又继续对问题进行研究,将“正方形”改为“矩形”、“菱形”和“任意平行四边形”(如图②、图③、图④),其它条件均不变,认为仍然有“EF⊥AE”.你同意小明的观点吗?若你同意小明的观点,请取图③为例加以证明;若你不同意小明的观点,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
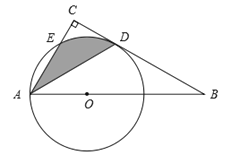
【题目】如图,Rt△ABC中,∠BAC=60°,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.
(1)求∠CAD的度数;
(2)若OA = 2,求阴影部分的面积(结果保留π).
【答案】(1)∠CAD的度数为30°;
(2)阴影部分的面积为![]() .
.
【解析】试题分析:(1)连接OD.由切线的性质可知OD⊥BC,从而可证明AC∥OD,由平行线的性质和等腰三角形的性质可证明∠CAD=∠OAD;(2)连接OE,ED、OD.先证明ED∥AO,然后依据同底等高的两个三角形的面积相等可知S△AED=S△EDO,于是将阴影部分的面积可转化为扇形EOD的面积求解即可.
试题解析:(1)连接OD,
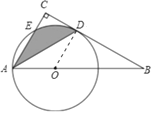
∵BC是⊙O的切线,D为切点,
∴OD⊥BC.
又∵AC⊥BC,
∴OD∥AC,
∴∠ADO=∠CAD.
又∵OD=OA,
∴∠ADO=∠OAD,
∴∠CAD=∠OAD=30°.
(2)连接OE,ED.

∵∠BAC=60°,OE=OA,
∴△OAE为等边三角形,
∴∠AOE=60°,
∴∠ADE=30°.
又∵![]() ,
,
∴∠ADE=∠OAD,
∴ED∥AO,
∴![]()
∴阴影部分的面积 = ![]() .
.
【题型】解答题
【结束】
6
【题目】如图是由两个长方体组合而成的一个立体图形的三视图,根据图中所标尺寸(单位:mm),求这个立体图形的表面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
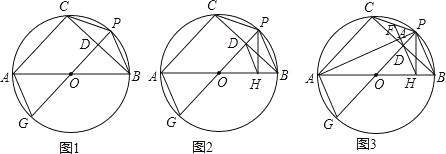
【题目】⊙O是△ABC的外接圆,AB是直径,过![]() 的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
(1)如图1,求证:AG=CP;
(2)如图2,过点P作AB的垂线,垂足为点H,连接DH,求证:DH∥AG;
(3)如图3,连接PA,延长HD分别与PA、PC相交于点K、F,已知FK=2,△ODH的面积为2![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
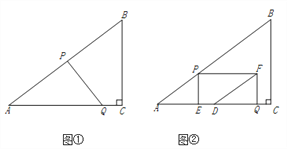
【题目】如图①,在Rt△ABC中,∠C=90°,AB=10,BC=6.点P从点A出发,沿折现AB—BC向终点C运动,在AB上以每秒5个单位长度的速度运动,在BC上以每秒3个单位长度的速度运动.点Q从点C出发,沿CA方向以每秒![]() 个单位长度的速度运动.点P、Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.
个单位长度的速度运动.点P、Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.
(1)求线段AQ的长.(用含t的代数式表示)
(2)当PQ与△ABC的一边平行时,求t的值
(3)如图②,过点P作PE⊥AC于点E,以PE、QE为邻边作矩形PEQF,点D为AC的中点,连结DF.直接写出DF将矩形PEQF分成两部分的面积比为1:2时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的推理过程,在括号内填上推理的依据,如图:

∵∠1+∠2=180°,∠2+∠4=180°(已知)
∴∠1=∠4( )
∴c∥a( )
又∵∠2+∠3=180°(已知 )
∠3=∠6( )
∴∠2+∠6=180°( )
∴a∥b( )
∴c∥b( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ∠B、∠D的两边分别平行。
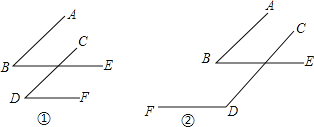
(1)在图1中,∠B与∠D的数量关系是 ;在图2中,∠B与∠FDC的数量关系是 ;
(2)用一句话归纳的结论为: ;
(3)已知∠α的两边与∠β的两边分别平行,并且∠α比∠β的3倍少![]() ,求∠α、∠β的度数.
,求∠α、∠β的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图1,抛物线y=﹣![]() x2﹣
x2﹣![]() x+3与x轴交于A和B两点(点A在点B的左侧),与y轴相交于点C,点D的坐标是(0,﹣1),连接BC、AC
x+3与x轴交于A和B两点(点A在点B的左侧),与y轴相交于点C,点D的坐标是(0,﹣1),连接BC、AC

(1)求出直线AD的解析式;
(2)如图2,若在直线AC上方的抛物线上有一点F,当△ADF的面积最大时,有一线段MN=![]() (点M在点N的左侧)在直线BD上移动,首尾顺次连接点A、M、N、F构成四边形AMNF,请求出四边形AMNF的周长最小时点N的横坐标;
(点M在点N的左侧)在直线BD上移动,首尾顺次连接点A、M、N、F构成四边形AMNF,请求出四边形AMNF的周长最小时点N的横坐标;
(3)如图3,将△DBC绕点D逆时针旋转α°(0<α°<180°),记旋转中的△DBC为△DB′C′,若直线B′C′与直线AC交于点P,直线B′C′与直线DC交于点Q,当△CPQ是等腰三角形时,求CP的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com