
【题目】如图1,在三角形ABC中,D是BC上一点,且∠CDA=∠CAB.(注:三角形内角和等于180°)

(1)求证:∠CDA=∠DAB+∠DBA;
(2)如图2,MN是经过点D的一条直线,若直线MN交AC边于点E,且∠CDE=∠CAD.求证:∠AED+∠EAB=180°;
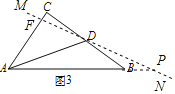
(3)将图2中的直线MN绕点D旋转,使它与射线AB交于点P(点P不与点A,B重合).在图3中画出直线MN,并用等式表示∠CAD,∠BDP,∠BPD这三个角之间的数量关系,不需证明.
【答案】(1)见解析;(2)见解析;(3)∠CAD=∠BDP+∠DPB.
【解析】
(1)根据三角形的内角和即可得到结论;
(2)根据三角形的内角和得到∠B=∠CDE,得到MN∥BA,根据平行线的性质证明;
(3)根据三角形的外角性质证明.
(1)∵∠C+∠CAD+∠ADC=∠C+∠CAB+∠B=180°,
∴∠CAD+∠ADC=∠CAB+∠B,
∵∠CDA=∠CAB,
∴∠CAD=∠B,
∵∠CAB=∠CAD+∠DAB=∠ABC+∠DAB,
∴∠CDA=∠DAB+∠DBA;
(2)∵∠CDA=∠CAB,∠C=∠C,
∴180°-∠CDA-∠C=180°-∠CAB -∠C
∴∠B=∠CAD,
∵∠CDE=∠CAD,
∴∠B=∠CDE,
∴MN∥BA,
∴∠AED+∠EAB=180°;
(3)∠CAD=∠BDP+∠DPB
证明:由三角形的外角的性质可知,∠ABC=∠BDP+∠DPB,
∵∠CDA=∠CAB,∠C=∠C,
∴∠B=∠CAD,
∴∠ABC=∠BDP+∠DPB.
∴∠CAD=∠BDP+∠DPB.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81,![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】威丽商场销售A、B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元?
(2)由于需求量大,A、B两种商品很快售完,威丽商场决定再一次购进A、B两种商品共34件,如果将这34件商品全部售完后所得利润不低于4000元,那么威丽商场至少需购进多少件A种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知P(1,2).
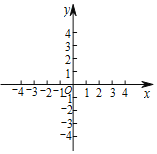
(1)在平面直角坐标系中描出点P(保留画图痕迹);
(2)如果将点P向左平移3个单位长度,再向上平移1个单位长度得到点P',则点P'的坐标为 .
(3)点A在坐标轴上,若S△OAP=2,直接写出满足条件的点A的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】右图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A、B、C、D,得到四边形ABCD.若AC=10cm,∠BAC=36°,则图中阴影部分的面积为( )
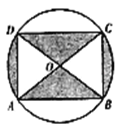
A. 5πcm2 B. 10πcm2 C. 15πcm2 D. 20πcm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件,其中甲种奖品每件40元,乙种奖品每件30元.
(1)如果购买甲、乙两种奖品共花费了650元,求甲、乙两种奖品各购买了多少件;
(2)如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过680元,求该公司有哪几种不同的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,![]() 是函数
是函数![]() 的图像上一点,
的图像上一点,![]() 是y轴上一动点,四边形ABPQ是正方形(点A.B.P.Q按顺时针方向排列)。
是y轴上一动点,四边形ABPQ是正方形(点A.B.P.Q按顺时针方向排列)。
(1)求a的值;
(2)如图②,当![]() 时,求点P的坐标;
时,求点P的坐标;
(3)若点P也在函数![]() 的图像上,求b的值;
的图像上,求b的值;
(4)设正方形ABPQ的中心为M,点N是函数![]() 的图像上一点,判断以点P.Q.M.N为顶点的四边形能否是正方形,如果能,请直接写出b的值,如果不能,请说明理由。
的图像上一点,判断以点P.Q.M.N为顶点的四边形能否是正方形,如果能,请直接写出b的值,如果不能,请说明理由。
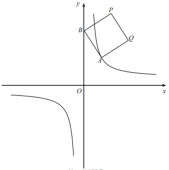
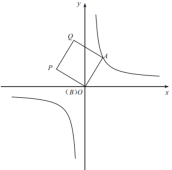

图① 图② 备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△AOB中,∠ABO=90°,OB=4,AB=8,直线y=-x+b分别交OA、AB于点C、D,且ΔBOD的面积是4.
(1)求直线AO的解析式;
(2)求直线CD的解析式;
(3)若点M是x轴上的点,且使得点M到点A和点C的距离之和最小,求点的坐标.
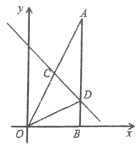
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com