
 阅读材料:关于三角函数还有如下的公式:
阅读材料:关于三角函数还有如下的公式:分析 (1)把15°化为45°-30°以后,再利用公式sin(α±β)=sinαcosβ±cosasinβ计算,即可求出sin15°的值;
(2)先根据锐角三角函数的定义求出BE的长,再根据AB=AE+BE即可得出结论.
解答 解:(1)sin15°=sin(45°-30°)=sin45°cos30°-cos45°sin30°=$\frac{\sqrt{2}}{2}$×$\frac{\sqrt{3}}{2}$-$\frac{\sqrt{2}}{2}$×$\frac{1}{2}$=$\frac{\sqrt{6}-\sqrt{2}}{4}$
(2)在Rt△BDE中,∵∠BED=90°,∠BDE=75°,DE=AC=7米,
∴BE=DE•tan∠BDE=DE•tan75°.
∵tan75°=2+$\sqrt{3}$,
∴BE=7(2+$\sqrt{3}$)=14+7$\sqrt{3}$,
∴AB=AE+BE=$\sqrt{3}$+14+7$\sqrt{3}$=14+8$\sqrt{3}$(米).
答:纪念碑的高度为(14+8$\sqrt{3}$)米.
点评 本题考查了:(1)特殊角的三角函数值的应用,属于新题型,解题的关键是根据题目中所给信息结合特殊角的三角函数值来求解.(2)解直角三角形的应用-仰角俯角问题,先根据锐角三角函数的定义得出BE的长是解题的关键.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4(80+x)=(80-x)×1 | B. | 80-x=4(80+x) | C. | 80+x=80-4x | D. | 80+x=4(80-x) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某居民楼紧挨一座山坡AB,经过地质人员勘测,当坡度不超过45°时,可以确保山体不滑坡,如图所示,已知AE∥BD,斜坡AB的坡角∠ABD=60°,.为防止滑坡,现对山坡进行改造,改造后,斜坡BC与地面BD成45°角,AC=20米.求斜坡BC的长是多少米?(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
某居民楼紧挨一座山坡AB,经过地质人员勘测,当坡度不超过45°时,可以确保山体不滑坡,如图所示,已知AE∥BD,斜坡AB的坡角∠ABD=60°,.为防止滑坡,现对山坡进行改造,改造后,斜坡BC与地面BD成45°角,AC=20米.求斜坡BC的长是多少米?(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
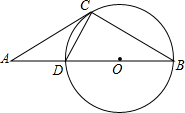 如图,点A是⊙O直径BD延长线上的一点,C在⊙O上,AC=BC,AD=CD
如图,点A是⊙O直径BD延长线上的一点,C在⊙O上,AC=BC,AD=CD查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com