
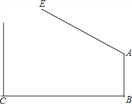
【题目】如图,甲,乙两人从点0出发去C地,甲的速度是乙速度的1.2倍,且甲在途中休息了半小时后仍按原速度行进.
(1)求甲,乙两人的行进速度.
(2)求线段BC的解析式,并写出定义域.
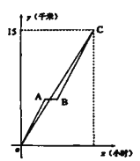
【答案】(1)甲速度6,乙速度5;(2)![]()
【解析】
(1) 根据图象信息,列方程求解即可;
(2)先求出C点坐标,设线段BC的解析式为y=6x+b,把C(3,15)代入得,利用待定系数法求线段BC的解析式即可.
解:(1)设乙的速度为x,则甲的速度为1.2x,根据图象信息,列方程得,
![]()
解得,x=5,
∴乙的速度为5千米/小时,甲的速度为6千米/小时;
(2) ∵乙的速度为5千米/小时,
∴点C的坐标为(3,15),
∵甲的速度为6千米/小时,
设线段BC的解析式为y=6x+b,把C(3,15)代入得,
15=6x+b,解得b=3,
∴线段BC的解析式y=6x3
∵甲在途中休息了半小时后仍按原速度行进,
∴x>![]() ,
,
∴定义域为![]() ,
,
∴线段BC的解析式![]()


 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
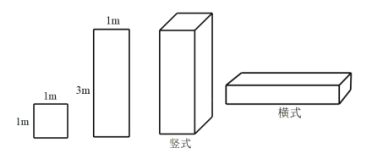
【题目】某工厂准备用图甲所示的![]() 型正方形板材和
型正方形板材和![]() 型长方形板材,制作成图乙所示的竖式和横式两种无盖箱子.
型长方形板材,制作成图乙所示的竖式和横式两种无盖箱子.
(1)若该工厂准备用不超过2400元的资金去购买![]() ,
,![]() 两种型号板材,制作竖式、横式箱子共10个,已知
两种型号板材,制作竖式、横式箱子共10个,已知![]() 型板材每张20元,
型板材每张20元,![]() 型板材每张60元,问最多可以制作竖式箱子多少只?
型板材每张60元,问最多可以制作竖式箱子多少只?
(2)若该工程新购得65张规格为![]() 型正方形板材,将其全部切割测好难过
型正方形板材,将其全部切割测好难过![]() 型或
型或![]() 型板材(不计损耗),用切割的板材制作两种类型的箱子,要求竖式箱子不少于10只,且材料恰好用完,则能制作竖式箱子______只.
型板材(不计损耗),用切割的板材制作两种类型的箱子,要求竖式箱子不少于10只,且材料恰好用完,则能制作竖式箱子______只.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)证明:不论![]() 取何值,该函数图像与
取何值,该函数图像与![]() 轴总有公共点;
轴总有公共点;
(2)若该函数的图像与![]() 轴交于点(0,3),求出顶点坐标并画出该函数图像;
轴交于点(0,3),求出顶点坐标并画出该函数图像;
(3)在(2)的条件下,观察图像,解答下列问题:
①不等式![]() 的的解集是 ;
的的解集是 ;
②若一元二次方程![]() 有两个不相等的实数根,则
有两个不相等的实数根,则![]() 的取值范围是 ;
的取值范围是 ;
③若一元二次方程![]() 在
在![]() 的范围内有实数根,则
的范围内有实数根,则![]() 的取
的取
值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现有甲种原料3600kg,乙种原料2410kg,计划利用这两种原料生产A,B两种产品共500件,产品每月均能全部售出.已知生产一件A产品需要甲原料9kg和乙原料3kg;生产一件B种产品需甲种原料4kg和乙种原料8kg.
(1)设生产x件A种产品,写出x应满足的不等式组.
(2)问一共有几种符合要求的生产方案?并列举出来.
(3)若有两种销售定价方案,第一种定价方案可使A产品每件获得利润1.15万元,B产品每件获得利润1.25万元;第二种定价方案可使A和B产品每件都获得利润1.2万元;在上述生产方案中哪种定价方案盈利最多?(请用数据说明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红家春天粉刷房间,雇用了5个工人,做了10天完工。用了某种涂料150升,费用为4800元;粉刷的面积为150![]() 。最后结算工钱时有以下几种方案:
。最后结算工钱时有以下几种方案:
方案1:按工算,每个工30元;(1个工人做一天是一个工)
方案2:按涂料费用算,涂料费用的30%作为工钱;
方案3:按粉刷面积算,每平方米付工钱12元。
请你帮小红家出主意,选择那种方案付钱最合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】几年前我国曾经流行有一种叫“二十四点”的数学趣味算题,方法是给出1~13之间的自然数,从中任取四个,将这四个数(四个数都只能用一次)进行“+”“-”“×”“÷”运算,可加括号使其结果等于24.
例如:对1,2,3,4可运算(1+2+3)×4=24,也可以写成4×(1+2+3)=24,但视作相同的方法.
现有郑、付两同学的手中分别握着四张扑克牌(见下图);若红桃、方块上的点数记为负数,黑桃、梅花上的点数记为正数.
请你对郑、付两同学的扑克牌的按要求进行记数,并按前面“二十四点”运算方式对郑、付两同学的记数分别进行列式计算,使其运算结果均为24.(分别尽可能提供多种算法)

依次记为:______ 、______ 、______ 、______

依次记为:______ 、______ 、______ 、______ .
(1)帮助郑同学列式计算:______
(2)帮助付同学列式计算:______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
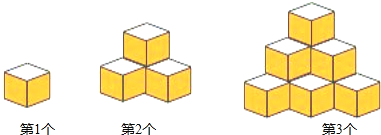
【题目】现用棱长为2cm的小立方体按如图所示规律搭建几何体,图中自上面下分别叫第一层、第二层、第三层…,其中第一层摆放1个小立方体,第二层摆放3个小立方体,第三层摆放6个小立方体…,那么搭建第1个小立方体,搭建第2个几何体需要4个小立方体,搭建第3个几何体需要10个小立方体…,按此规律继续摆放.
(1)搭建第4个几何体需要小立方体的个数为 ;
(2)为了美观,需将几何体的所有露出部分(不包含底面)都喷涂油漆,且喷涂1cm2需用油漆0.2克.
①求喷涂第4个几何体需要油漆多少克?
②如果要求从第1个几何体开始,依此对第1个几何体,第2个几何体,第3和几何体,…,第n个几何体(其中n为正整数)进行喷涂油漆,那么当喷涂完第21个几何体时,共用掉油漆多少克?
(参考公式:①1×2+2×3+3×4+…+n(n+1)=![]() ;
;
②12+22+32+…+n2=![]() ,其中n为正整数)
,其中n为正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校大门出口处有一自动感应栏杆,点A是栏杆转动的支点,当车辆经过时,栏杆AE会自动升起,某天早上,栏杆发生故障,在某个位置突然卡住,这时测得栏杆升起的角度∠BAE=127°,已知AB⊥BC,支架AB高1.2米,大门打开的宽度BC为2米,以下哪辆车可以通过?(栏杆宽度,汽车反光镜忽略不计)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.车辆尺寸:长×宽×高)( )
A. 宝马Z4(4200mm×1800mm×1360mm) B. 奔驰smart(4000mm×1600mm×1520mm)
C. 大众朗逸(4600mm×1700mm×1400mm) D. 奥迪A6L(4700mm×1800mm×1400mm)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com