(1)∵AB是⊙O的直径(已知)∴∠ACB=90º(直径所对的圆周角是直角)
∵∠ABC=60º(已知)
∴∠BAC=180º-∠ACB-∠ABC= 30º(三角形的内角和等于180º)
∴AB=2BC=4cm(直角三角形中,30º锐角所对的直角边等于斜边的一半)即⊙O的直径为4cm.
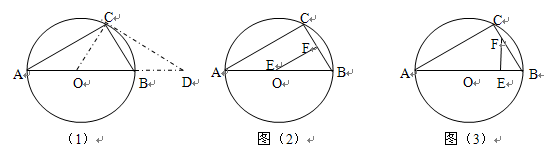
(2)如图10(1)CD切⊙O于点C,连结OC,则OC=OB=1/2·AB=2cm.
∴CD⊥CO(圆的切线垂直于经过切点的半径)∴∠OCD=90º(垂直的定义)
∵∠BAC= 30º(已求)
∴∠COD=2∠BAC= 60º(在同圆或等圆中一条弧所对的圆周角等于它所对的圆心角的一半)
∴∠D=180º-∠COD-∠OCD= 30º(三角形的内角和等于180º)
∴OD=2OC=4cm(直角三角形中,30º锐角所对的直角边等于斜边的一半)
∴BD=OD-OB=4-2=2(cm)
∴当BD长为2cm,CD与⊙O相切.
(3)根据题意得:BE=(4-2t)cm,BF=tcm;
如图10(2)当EF⊥BC时,△BEF为直角三角形,此时△BEF∽△BAC
∴BE:BA=BF:BC
即:(4-2t):4=t:2 解得:t=1
如图10(3)当EF⊥BA时,△BEF为直角三角形,此时△BEF∽△BCA
∴BE:BC=BF:BA
即:(4-2t):2=t:4 解得:t=1.6
∴当t=1s或t=1.6s时,△BEF为直角三角形.
(1)根据已知条件知:∠BAC=30°,已知AB的长,根据直角三角形中,30°锐角所对的直角边等于斜边的一半可得AB的长,即⊙O的直径;
(2)根据切线的性质知:OC⊥CD,根据OC的长和∠COD的度数可将OD的长求出,进而可将BD的长求出;
(3)应分两种情况进行讨论,当EF⊥BC时,△BEF为直角三角形,根据△BEF∽△BAC,可将时间t求出;
当EF⊥BA时,△BEF为直角三角形,根据△BEF∽△BCA,可将时间t求出.

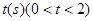 ,连结EF,当
,连结EF,当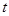 为何值时,△BEF为直角三角形.
为何值时,△BEF为直角三角形.