
【题目】已知△ABC∽△DEF , 且相似比为4:3,若△ABC中BC边上的中线AM=8,则△DEF中EF边上的中线DN=。
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC,其中正确结论的个数为( )
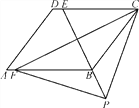
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4.则下列结论错误的是( ).

A.AE∥BC B. ∠ADE=∠BDC
C.△BDE是等边三角形 D. △ADE的周长是9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,∠BOD=45°,按下列要求画图并回答问题: 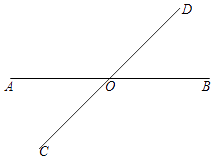
(1)利用三角尺,在直线AB上方画射线OE,使OE⊥AB;
(2)利用圆规,分别在射线OA、OE上截取线段OM、ON,使OM=ON,连接MN;
(3)利用量角器,画∠AOD的平分线OF交MN于点F;
(4)直接写出∠COF=°.
查看答案和解析>>
科目:初中数学 来源: 题型:
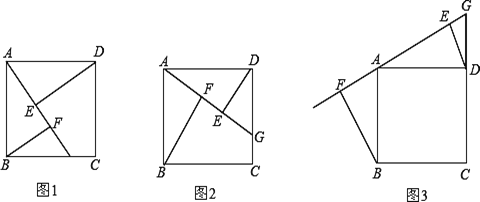
【题目】四边形ABCD是正方形(提示:正方形四边相等,四个角都是90°)
如图1,点G是BC边上任意一点(不与点B、C重合),连接AG,作BF⊥AG于点F,
DE⊥AG于点E.求证:△ABF≌△DAE;
(2) ①如图2,若点G是CD边上任意一点(不与点C、D重合),连接AG,作BF⊥AG于点F,
DE⊥AG于点E,线段EF与AF、BF的等量关系是______ ___;
②如图3,若点G是CD延长线上任意一点,连接AG,作BF⊥AG于点F,DE⊥AG于点E,
线段EF与AF、BF的等量关系是______ ;
(3)若点G是BC延长线上任意一点,连接AG,作BF⊥AG于点F,DE⊥AG于点E,请画图并
探究线段EF与AF、BF的等量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
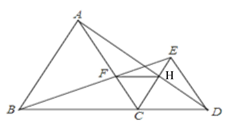
【题目】已知:点B,C,D在同一直线上,△ABC和△CDE都是等边三角形,BE交AC于点F,AD交CE于点H,
(1)求证:△BCE≌△ACD;
(2)判断△CFH的形状并说明理由.
(3)写出FH与BD的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com